


一次関数の式や座標を求める練習問題:基本レベル
点(2,1)を通り、傾きが-4の直線の式を求めよ。
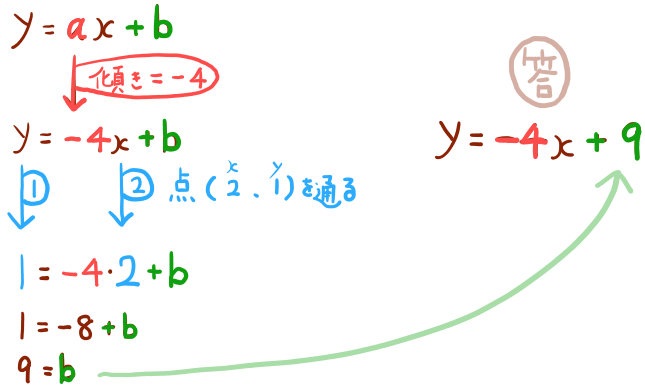









この関数が\(x=5\) のときのyの値を求めよ。
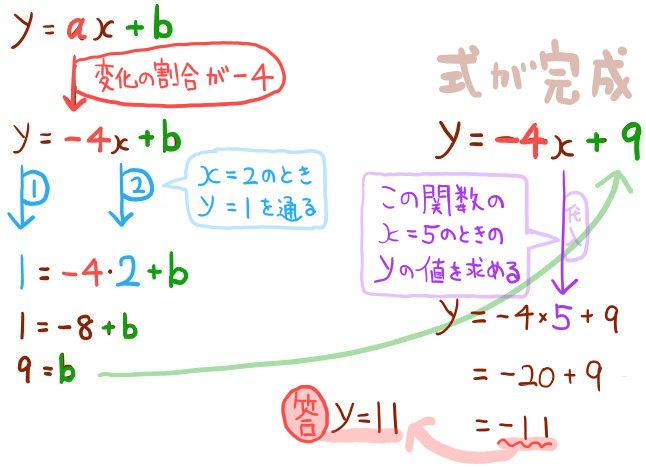
答え:y=-11




変化の割合が\(\dfrac{3}{2}\)で、\(x=4\) のとき \(y=10\) となる直線の式を求めよ。
 変化の割合は、一次関数の場合、傾きの値としてそのまま使えます。
変化の割合は、一次関数の場合、傾きの値としてそのまま使えます。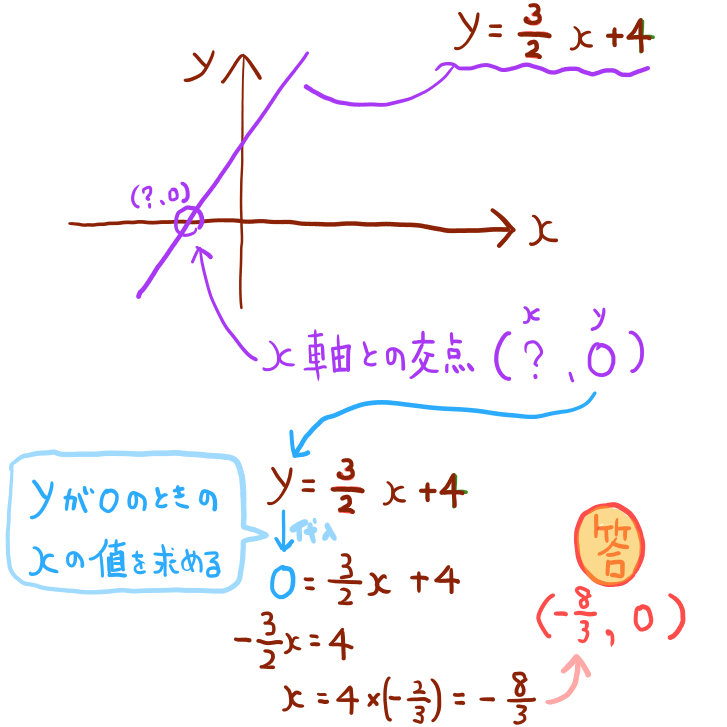
このグラフがx軸と交わる、ということは、その交点の座標は(?、0)ということまではわかります。
つまりx軸との交点のy座標は0ということなので、一次関数の式のyに0を代入してあげると、その交点のx座標が求められる、ということになります。
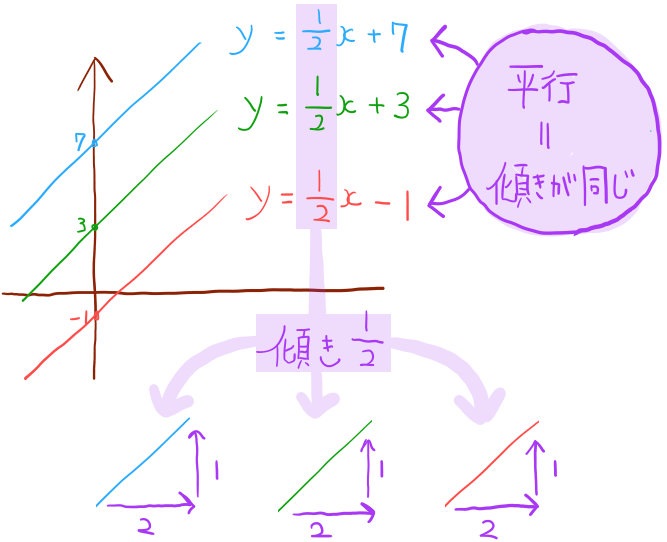
\(y=\dfrac{1}{2}x+3\) に平行で、\(x=4\) のとき \(y=10\) となる一次関数の式を求めよ。

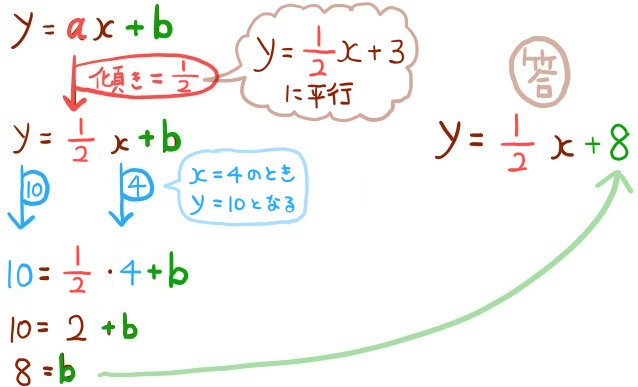
2点(a,11)、(4,10)を通る一次関数のグラフは \(y=\dfrac{1}{2}x-1\) に平行である。aの値を求めよ。
それが点(a,11)を通る、ということなので、\(y=\dfrac{1}{2}x+8\) のyに11を代入してxを求めると、x=6となります。
つまり点(6,11)を通る、ということなので、aは6ということになります。
切片が5である一次関数のグラフが、点(4,3)を通る。この一次関数の式を求めよ。
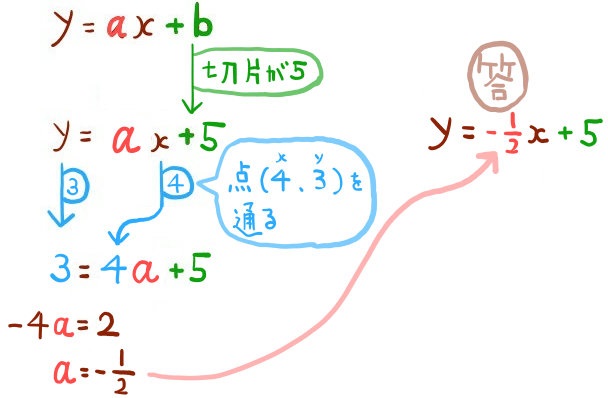
 傾きの値=\(\dfrac{yの増加量}{xの増加量}\)を使います。
傾きの値=\(\dfrac{yの増加量}{xの増加量}\)を使います。
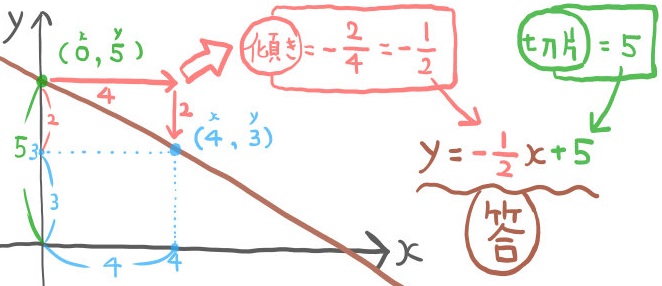
グラフを通る2点の座標から、それぞれの増加量を調べます。
傾きの値=\(\dfrac{-2}{4}\)なので、傾きは\(-\dfrac{1}{2}\)となります。
このようにグラフを書いて傾きを求めると、意味がわかりながら解くことができます。
 直線の方程式を求めたのち、グラフとx軸との交点を求めます。
直線の方程式を求めたのち、グラフとx軸との交点を求めます。
グラフとx軸との交点は、y座標の値が0なので、直線の方程式のyの値に0を代入して、y=0のときのxの値を求めます。
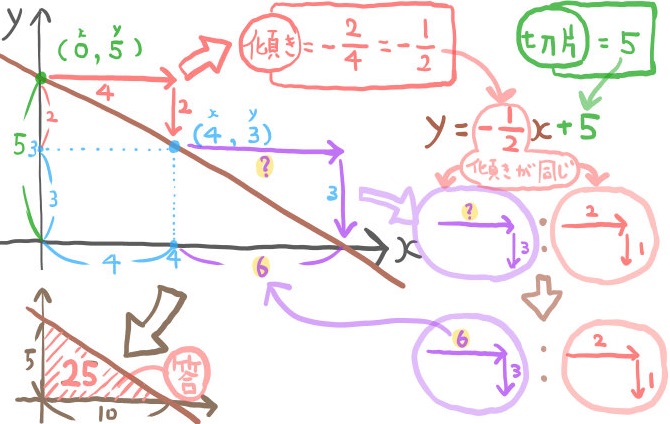
xの値が10と出ましたので、上の図のように求める図形の底辺の長さが10ということがわかりました。
図の4本の直線A、B、C、Dについての式をそれぞれ求めよ。
 グラフとy軸との交点のy座標の値がy切片となりますので、そこから求めるのが早いでしょう。
グラフとy軸との交点のy座標の値がy切片となりますので、そこから求めるのが早いでしょう。
あとは傾きをグラフから求めて式の完成です。
 その図のように4通りの方法が考えられます。
その図のように4通りの方法が考えられます。2点(2,4)、(8,7)を通る一次関数の式を求めよ。
 2点を通る直線の方程式を求める場合の最もオーソドックスな方法は連立方程式による解法です。
2点を通る直線の方程式を求める場合の最もオーソドックスな方法は連立方程式による解法です。
図のように二通りの式をつくり、連立方程式でaとbの値を求めて、式を完成させます。
 傾きを先に求める方法です。このように、グラフ上で考えると、何をやっているのかわかりやすいと思います。
傾きを先に求める方法です。このように、グラフ上で考えると、何をやっているのかわかりやすいと思います。2点(-4,1)、(2,4)を通る一次関数の式を求めよ。


3点(-4,1)、(2,a)、(8,7)を通る一次関数がある。aの値を求めよ。


直線ℓ:\(y=3x+6\) と、直線m: \(y=-\dfrac{1}{2}x-1\) の交点の座標を求めよ。
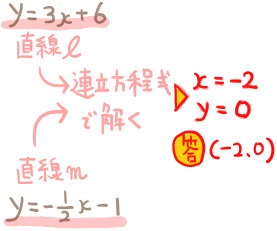 2直線の交点の座標を求めるためには、連立方程式で求める、という手順が一般的な方法です。
2直線の交点の座標を求めるためには、連立方程式で求める、という手順が一般的な方法です。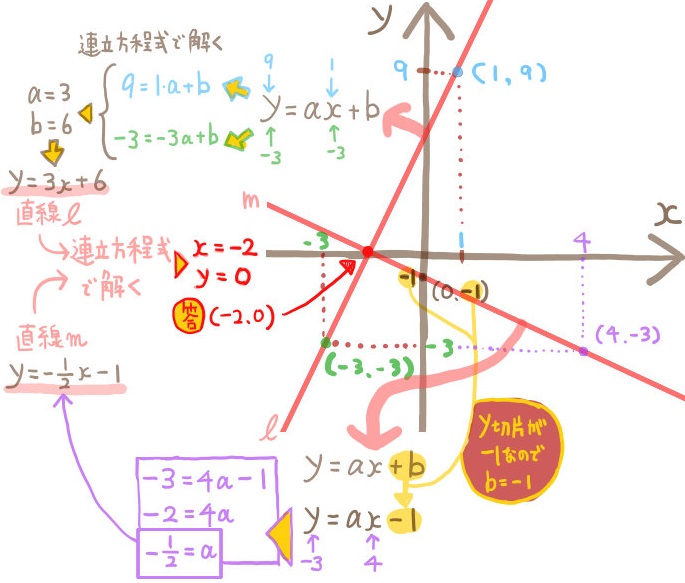 これはさっきの問題のように、式が直接あたえられていない場合のケースです。
これはさっきの問題のように、式が直接あたえられていない場合のケースです。
2点を通る、という情報から、それぞれの式を求めてから連立方程式で交点の座標を求めるという手順を踏みます。

一次関数:変化の割合=\(\dfrac{yの増加量}{xの増加量}\)の練習問題
\(y=2x+3\) のxの増加量が5のときのyの増加量を求めよ。

変化の割合=\(\dfrac{yの増加量}{xの増加量}\)なので、それぞれに該当する数値を代入します。
この問題の場合は、傾きが2とありますので、変化の割合のところに2を代入します。
xの増加量が5とありますので、それも代入します。
すると、その場合のyの増加量を求める方程式が完成します。
\(y=\dfrac{1}{3}x+1\) のxが3から21まで増加するときのyの増加量を求めよ。

\(y=\dfrac{1}{3}x+1\) のyの増加量が6のときのxの増加量を求めよ。

一次関数:変域の練習問題
\(y=2x+3\) のxの変域が、4≦x≦8のときのyの変域を求めよ。
 変域とは、簡単に言えば、どこからどこまでの話かを限定する範囲のことです。
変域とは、簡単に言えば、どこからどこまでの話かを限定する範囲のことです。




上の図を見ると、一番高いy座標は19で、一番低いy座標は11ということがわかりますね。
なのでyの変域は11≦y≦19ということです。


xが8の時のyの値を求めるとyが19だと計算で出てきますよね。
\(y=2x+3\)のyの変域が、11≦y≦19となるようなxの変域を求めよ。

\(y=-\dfrac{1}{2}x+16\) のxの変域が、-2≦x≦2のときのyの変域を求めよ。
 傾きが-になっているとミスをする確率が増えます。
傾きが-になっているとミスをする確率が増えます。


どうしてこういうミスが起こるのかという言うと、グラフを書かないで答えを出そうとするからです。

xに-2を代入して求めたyの値17は左に
xに2を代入して求めたyの値15は右に
書いておけばいいじゃん!→(17≦y≦15)
として間違うパターンです。
このミスを防ぐ方法はただひとつ、『グラフと変域を書いてそれを見ながら解答を出す』という手順を踏むことです。
特に変域の問題は今回のように一次関数だけでなく、反比例や二次方程式などにも登場します。































