

にゃんこ
このページでは、様々な相似比の求め方を学習できます。
このページの内容
- 相似比の求め方|辺の長さに小数がある問題
- 相似比の求め方|向きがそろっていない四角形や多角形の問題
- 円の相似比の求め方
相似比の求め方|辺の長さに小数がある問題
問題
次の図において、△ABC∽△DEFである。
AB=5、DE=8.2であるとき、△ABCと△DEFの相似比を求めよ。
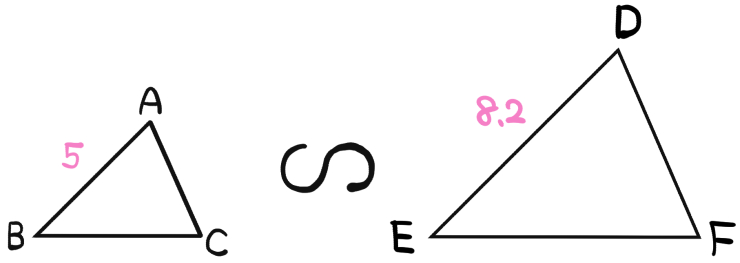

にゃんこ
このように「相似比を求めよ」と言われたら、基本的に「最も簡単な整数の比で表して答えよ」というルールまでセットになっていると思ってください。
求め方
相似比の求め方|向きがそろっていない四角形や多角形の問題
問題
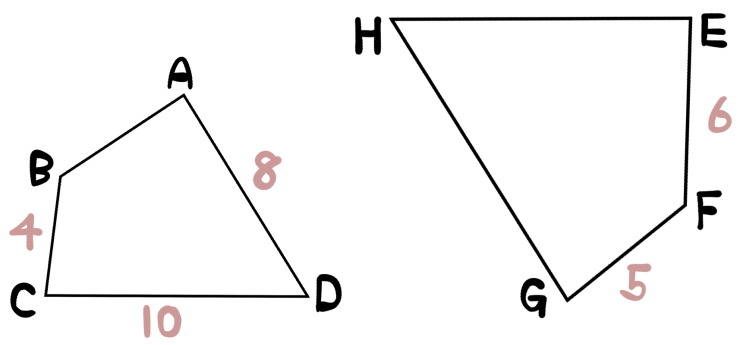
次の図において、四角形ABCD∽四角形EFGHである。
明らかになっている辺の長さは、図の通りである。
このとき、四角形ABCDと四角形EFGHの相似比を求めよ。

にゃんこ
この問題のように、四角形または多角形の場合は、どの辺とどの辺が対応しているのか、発見しにくいと思います。

坂田先生
対応する辺の見つけ方は3つあります。
対応する辺の見つけ方3通り
見つけ方1:二つの図形の向きをそろえてから考える
見つけ方2:相似を表す関係式に辺の長さを書き込む
見つけ方3:長さの順番に注目して見つける

にゃんこ
では順番に見ていきます。
見つけ方1:二つの図形の向きをそろえてから考える
四角形の向きをそろえることで、対応する辺がどことどこなのかを見つけやすくします。
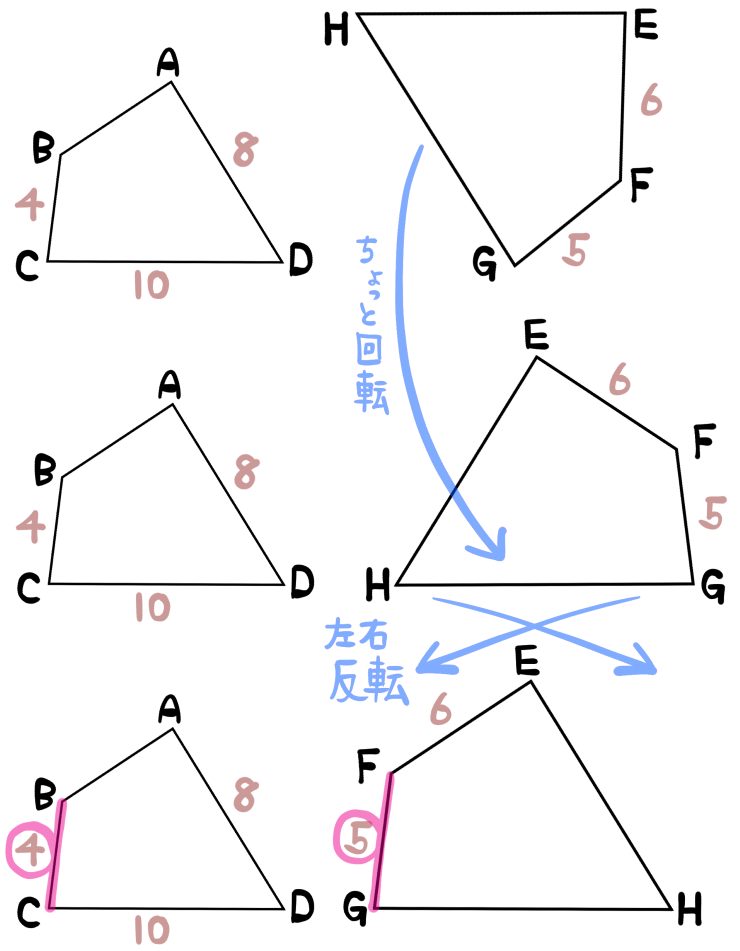


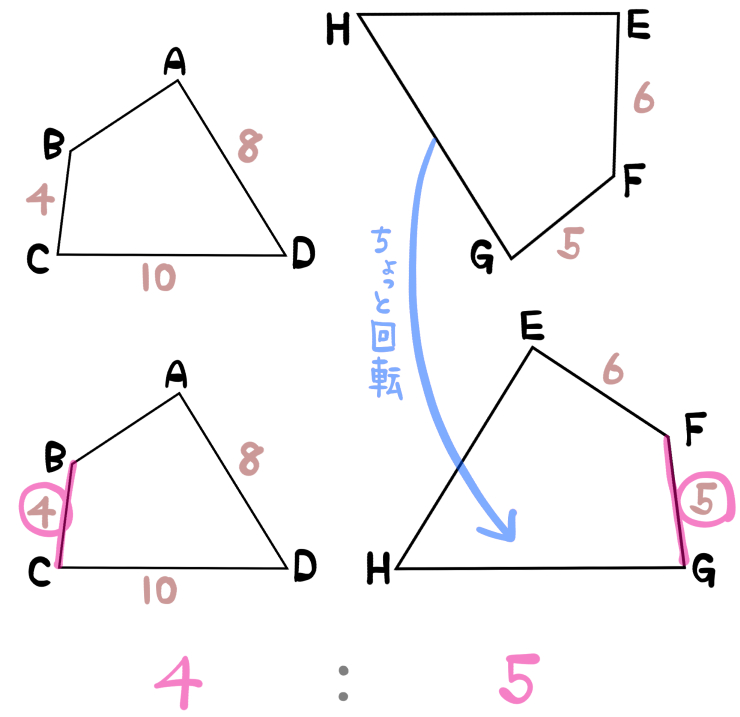

1:回転だけで向きがそろう場合
2:回転+裏返しで向きがそろう場合(この問題)
の2パターンあります。


にゃんこ
このようにして求めます。

坂田先生
ちなみに、回答できるなら、このように回転だけで答えてもいいでしょう。

見つけ方2:相似を表す関係式に辺の長さを書き込む
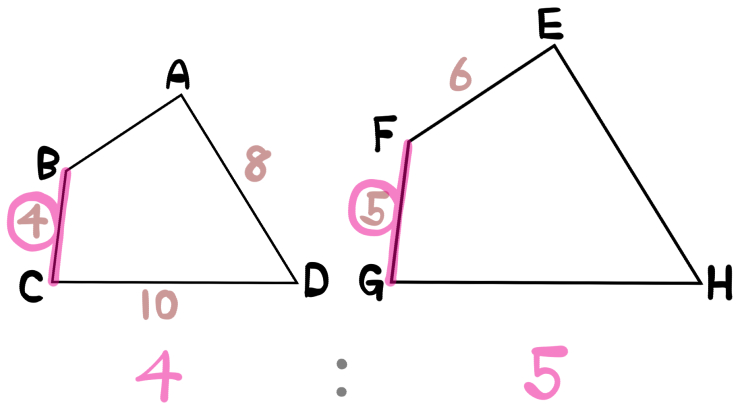
まず、相似を表す関係式と図を見ながら、次のように、わかっている辺の長さを書き込みます。

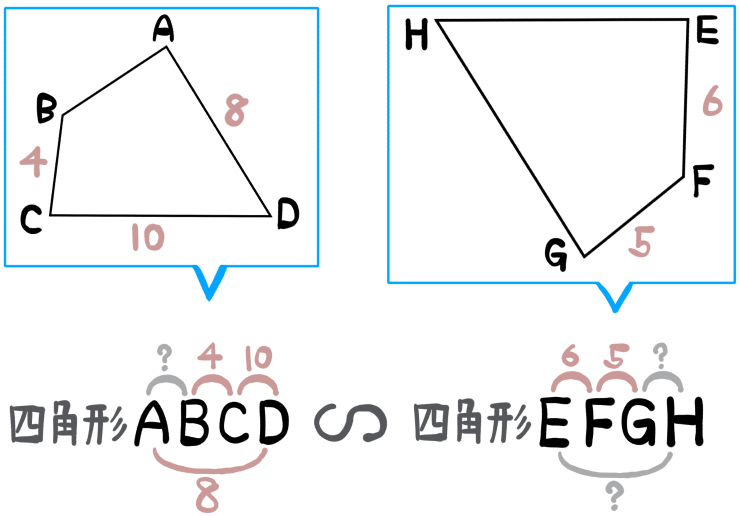
そもそもABCD、EFGHという並びは、それぞれの頂点や辺が対応する順番で書かれています。
ということは、同じ位置に書き込めた4と5が、対応する辺の長さになっているということです。


にゃんこ
よって4:5が相似比だとわかります。
注意点
結構便利なワザですが、「四角形ABCD∽四角形EFGH」ということが問題文に書かれている場合のみ使えるテクニックです。
「相似な2つの四角形がある」とだけ書かれていた場合は使えません。
「相似な2つの四角形がある」とだけ書かれていた場合は使えません。
見つけ方3:長さの順番に注目して見つける

坂田先生
何番目に長い辺なのかを手掛かりに、相似比を求める方法もあります。
一番長い辺、一番短い辺を最初に探します。
次に2番目に長い辺、2番目に短い辺、というように探していくと見つけやすいです。
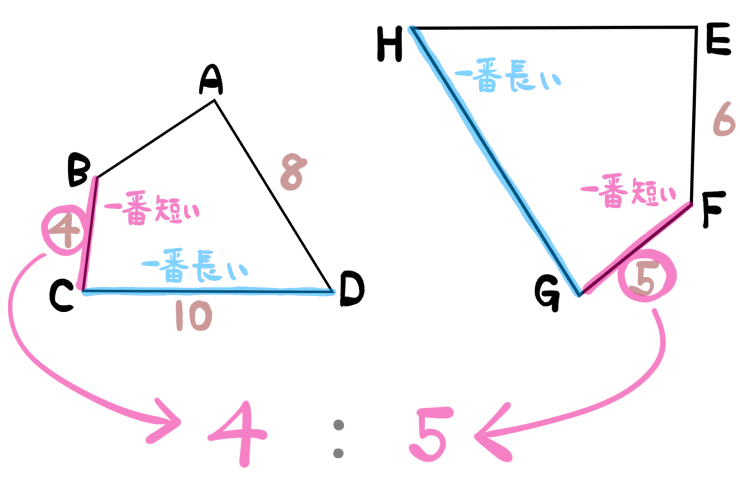
この問題の場合は、一番短い辺の長さがともにわかっていたので、相似比を求めることができました。

坂田先生
このように、長さの順番がはっきりわかる図形なら、それを手掛かりに相似比を求められる場合があります。

にゃんこ
ただし、辺の長さがわかっている部分が、何番目の長さなのかがわかりにくい図形である場合、この方法は使えません。
円の相似比の求め方

坂田先生
円の相似比は、次の3つのうちの1つでもわかると、求めることができます。
1:半径の長さの比
2:直径の長さの比
3:円周の長さの比
これらの比はすべて同じであり、相似比でもあります。
2:直径の長さの比
3:円周の長さの比
これらの比はすべて同じであり、相似比でもあります。

にゃんこ
例として、半径が2:3の二つの円について見てみましょう。
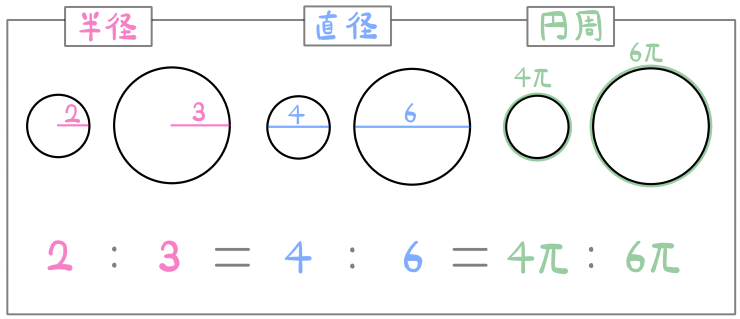
・半径の比
・直径の比
・円周の比
そのどれもが2:3(相似比)になることがわかります。
・直径の比
・円周の比
そのどれもが2:3(相似比)になることがわかります。

にゃんこ
円周の比が本当に2:3になるのかわからない方は、この式変形を見てください。
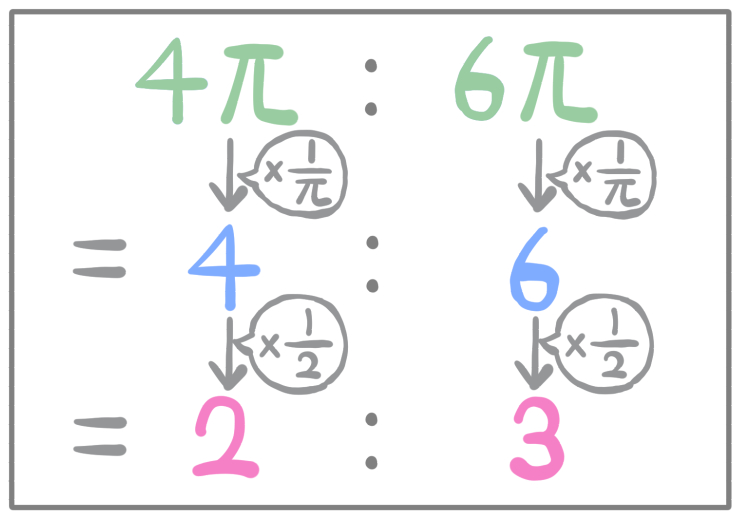

坂田先生
半径、直径、円周の比が同じになる理由も、ちょっとわかったかもしれませんね。もう少し確認してみましょう。
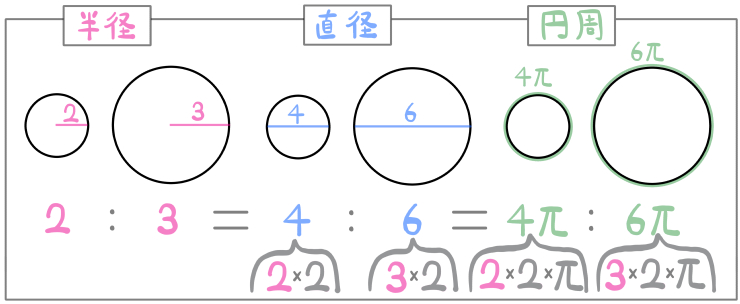
直径は、半径の長さをそれぞれ2倍しただけなので、比は同じままになりますね。
円周も、半径の長さをそれぞれ2π倍しただけなので、比は同じままです。





























10倍することにより、5:8.2が50:82になります。
これにより、50:82が25:41になります。