坂田先生
このページでは、以下の共通因数でくくりだす因数分解の問題を徹底的に練習できます。
にゃんこ
この問題&解答をプリントアウトしておきたい方は50問目の最後をご覧ください。
文字の共通因数をくくりだす因数分解の問題｜中学基礎レベル
坂田先生
中学数学の因数分解を解く基礎となる土台を作り、難関私立高校入試に対応できる応用レベルまで養うことができます。
答えの確認方法
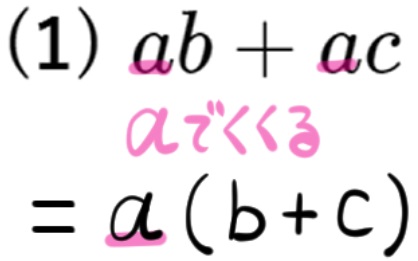
共通因数でくくりだした後の式変形が合っているかどうかは、その変形後の式を展開してみて、もとの式と一致するかどうかということを確認してみるといいでしょう。
(2) \(ab-ac\)
1がなぜ登場するか？
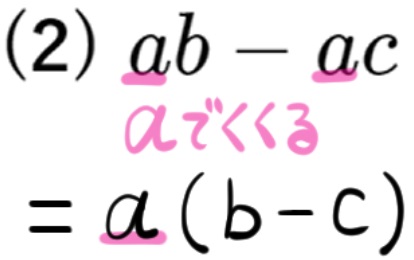
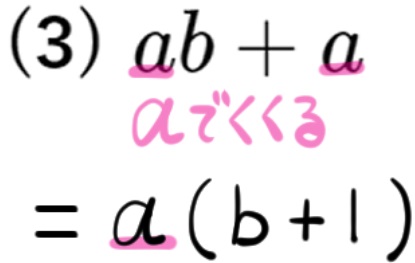
上の問題でくくりだしのあと\(a\left( b+1\right) \) となっていますが、そのなかの1の部分は0じゃないの？と思った方は\(a\left( b+1\right) \) を展開して、もとの式と一致するかどうかを調べてみてください。
(4) \(ab-a\)
項が３つある場合の共通因数
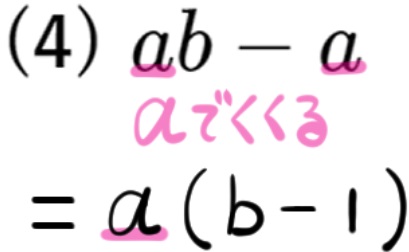
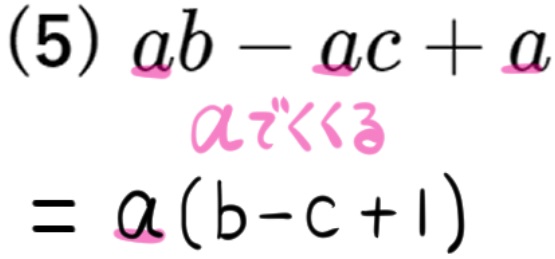
このように項が３つある場合も、すべての項に共通する因数（この場合はa）でくくりだすことができます。
(6) \(a^{2}b+a\)
複数の文字パターン
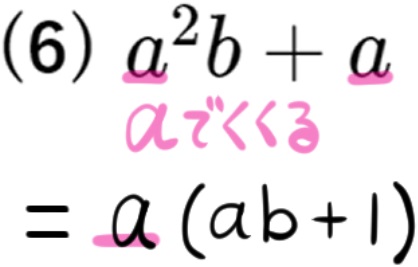
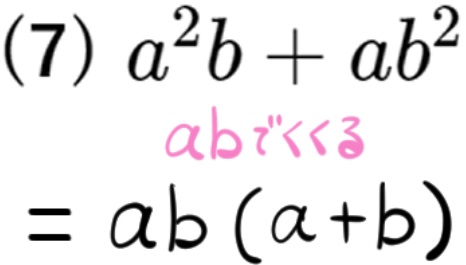
共通因数に複数の文字がある場合はそれらをまとめてくくりだすということをします。そのパターンが少し続きます。
(8) \(a^{2}b+a^{2}c\)
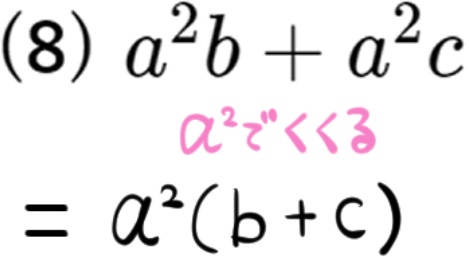
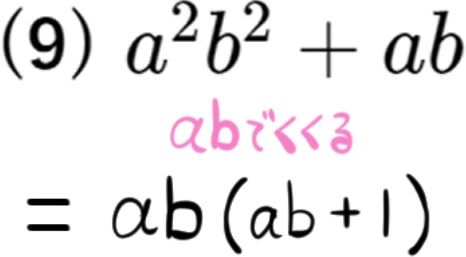
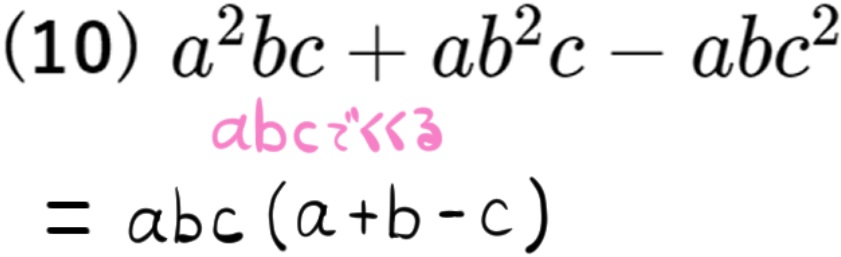
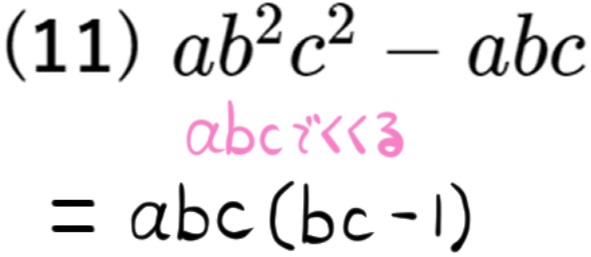
数や文字の共通因数をくくりだす問題｜基礎～標準レベル
(12) \(2a+2b\)
この場合の共通因数は２となります。
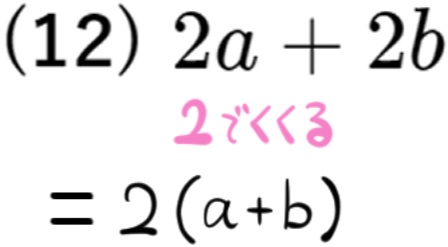
(13) \(2a-6b\)
２と６の最大公約数である２でくくりだします。
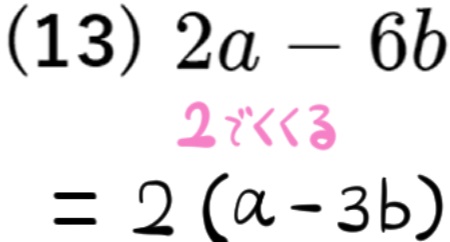
(14) \(2a+7a^{2}\)
２と７の最大公約数は１なので、数でくくりだすことはせず文字だけを共通因数とし、因数分解します。
２と６の最大公約数は２なので、さらにaも共通因数としてあるので、2aをくくります。
これも2aをくくります。2aの項を2aでくくりだすと1になります。しっくりこない場合は、答えのかたちを展開して、もとの式にもどしてみてください。
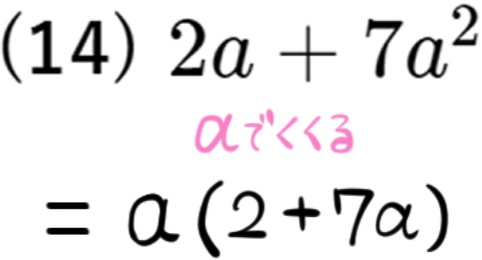
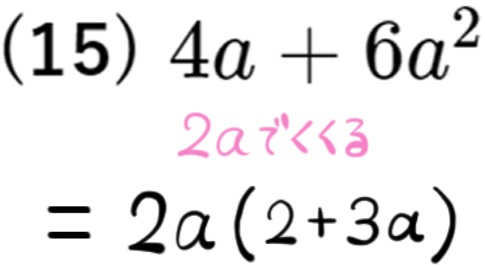
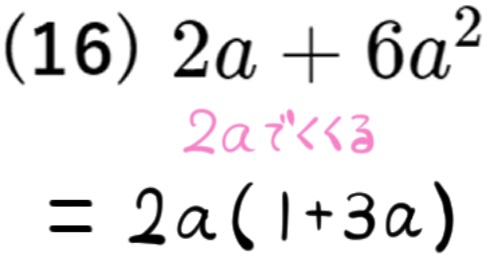
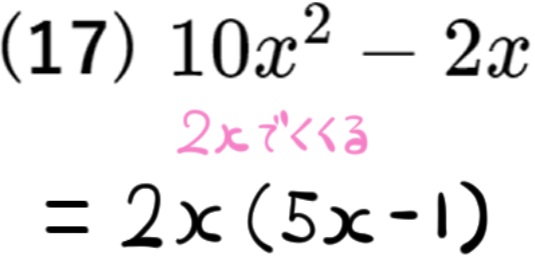
おきかえを利用して共通因数をくくりだす問題｜標準～応用
坂田先生
ここからはおきかえを利用して共通因数をくくりだす問題も登場します。
a+bをMにおきかえ因数分解しやすいようにしています。難関私立などを目指す方は、慣れてきたら、文字におきかえずに同じ操作ができるように練習してみてください。
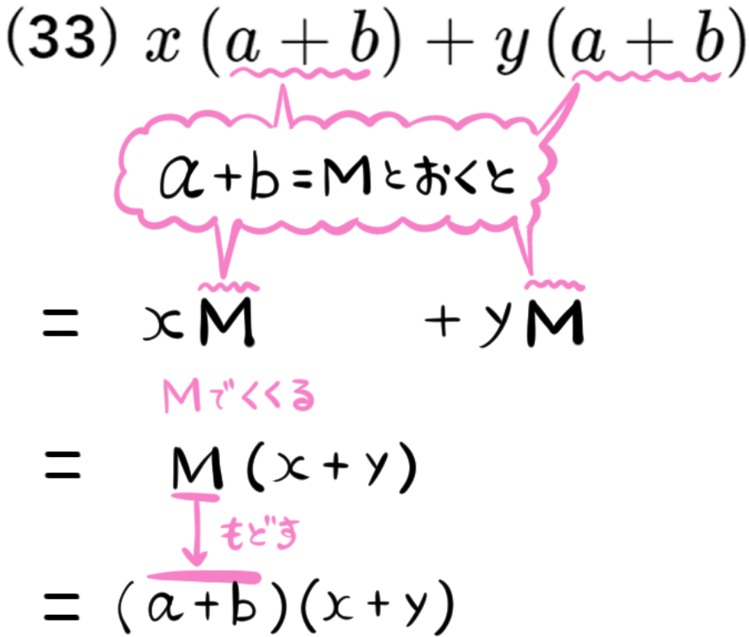
(36) \(\left( a+b\right) ^{2}+\left( a+b\right) \)
文字におきかえる場合、この文字にしないといけない、というルールはありません。ただ、同じアルファベットの大文字と小文字が混ざる式になるような、ややこしい文字は使わないほうがいいでしょう。
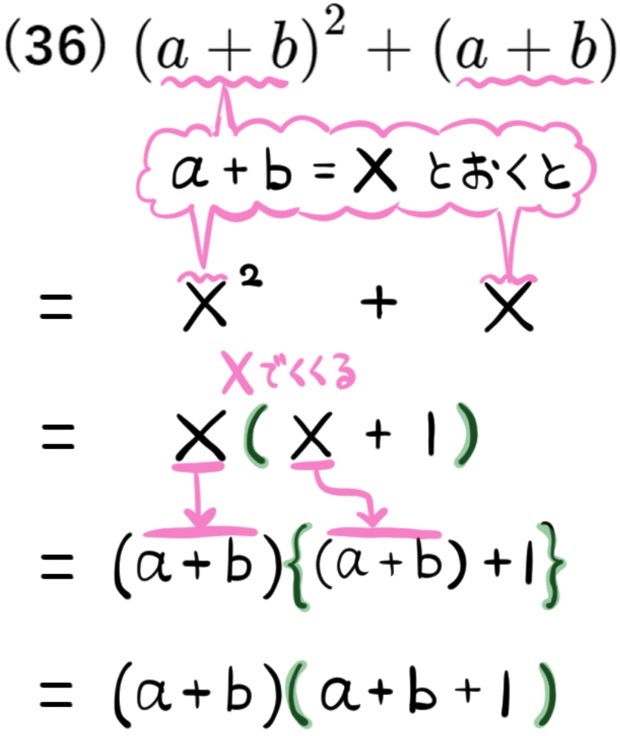
式の一部をくくりだす操作が必要になる因数分解の問題
(39) \(a^{2}\left( x+2\right) +x+2\)
同じ項のならびが作れるように、式の一部を-1でくくりました。このように、式の一部をくくりだしによって変形する操作で因数分解する問題もあります。
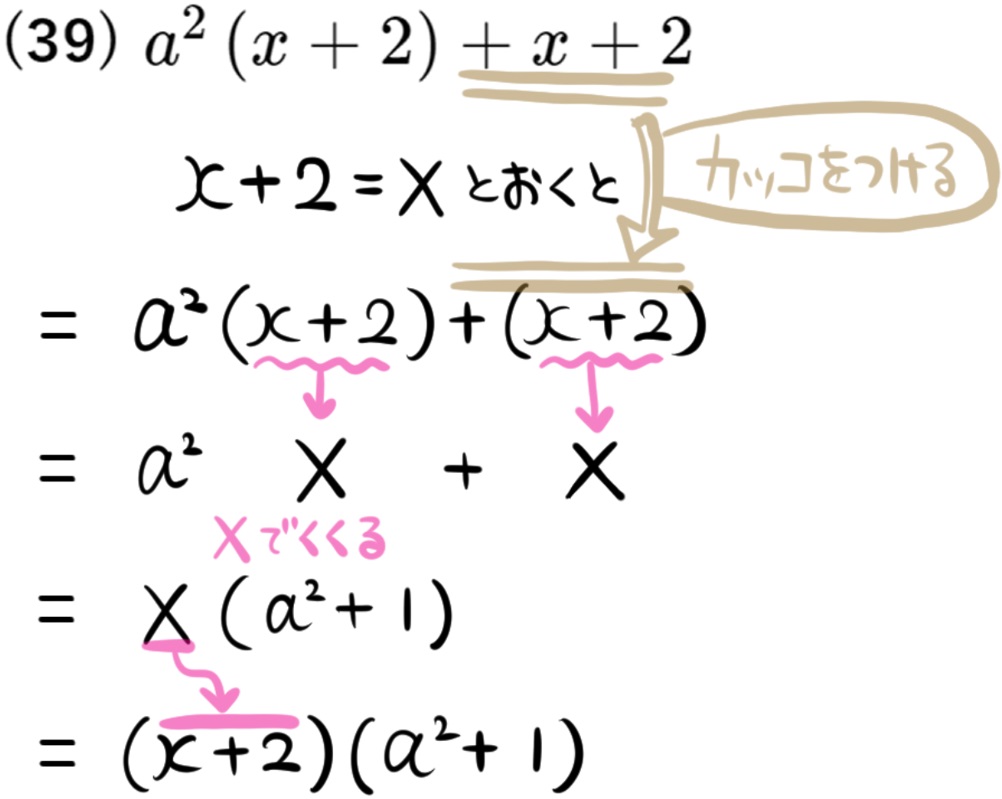
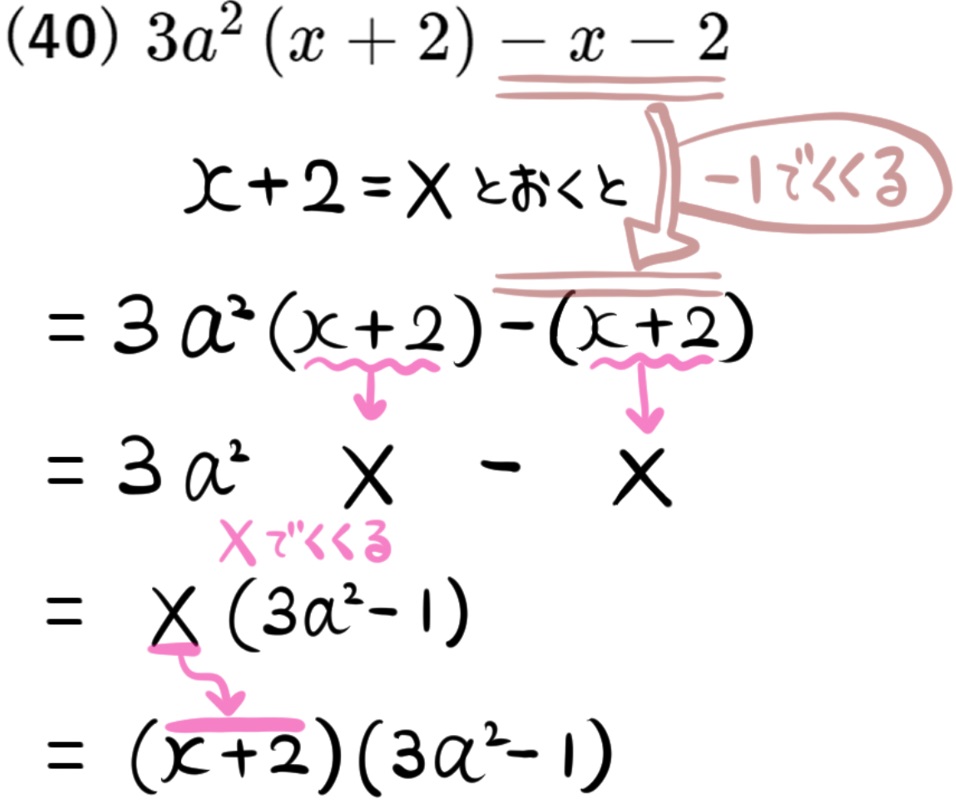
(41) \(3a^{2}\left( x+2\right) -2x-4\)
式の一部を共通因数でくくりだすという操作を二カ所で実行するパターンの問題です
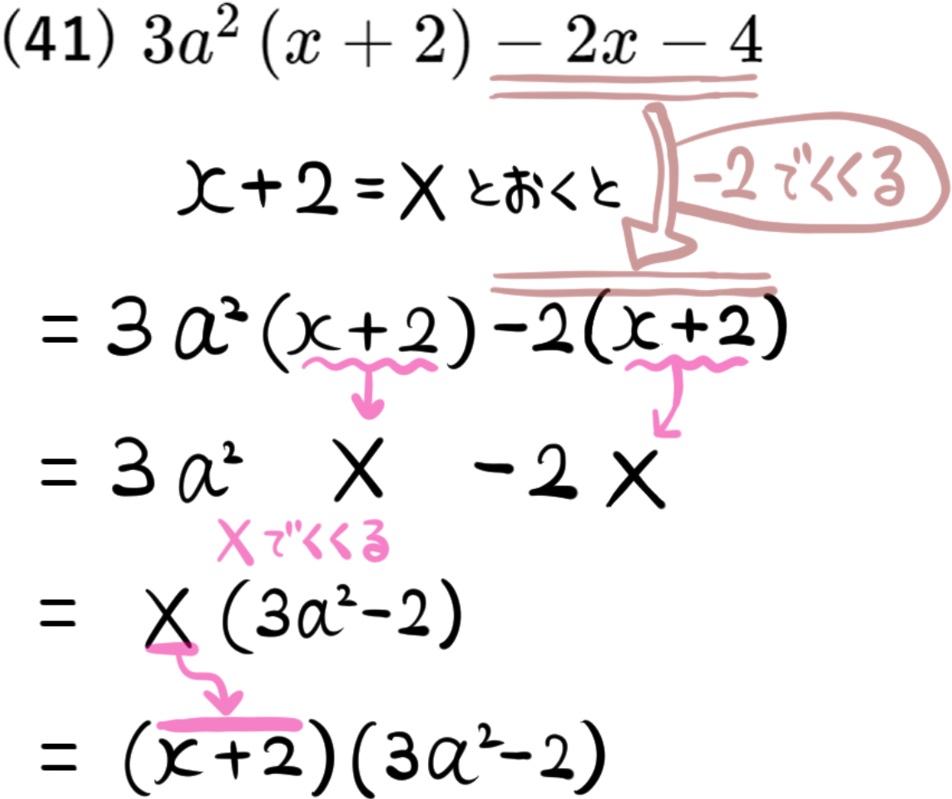
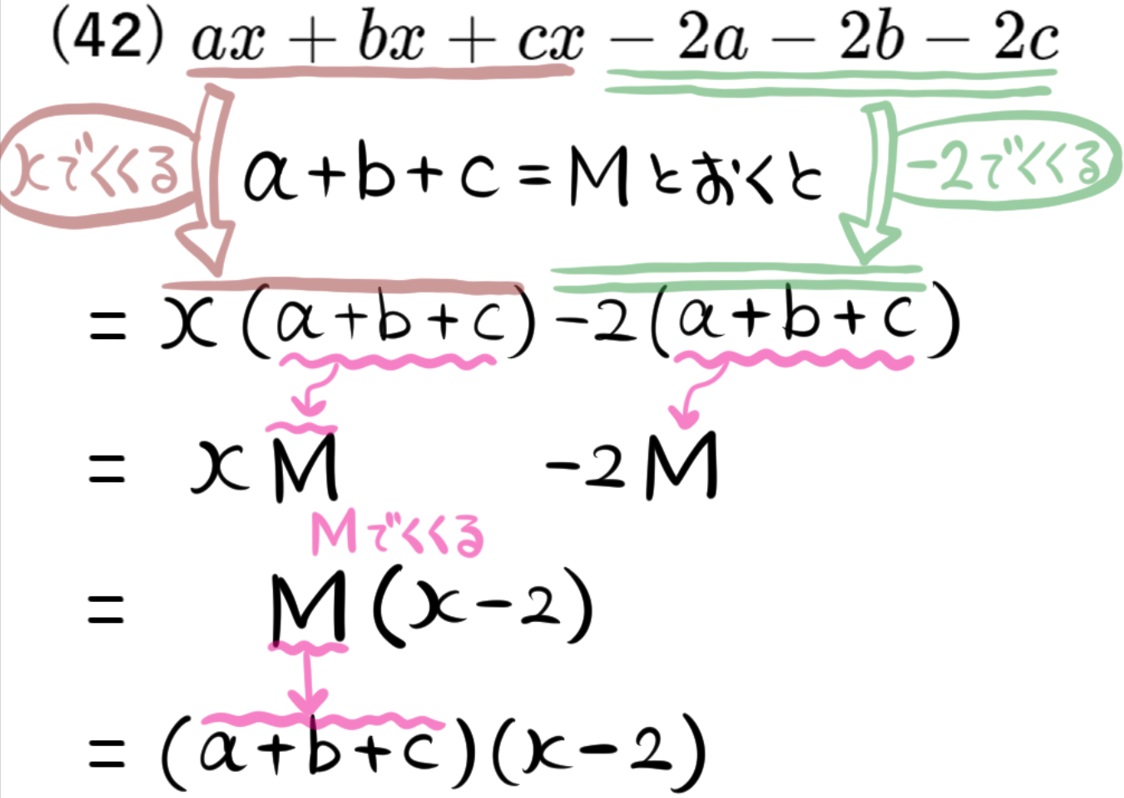
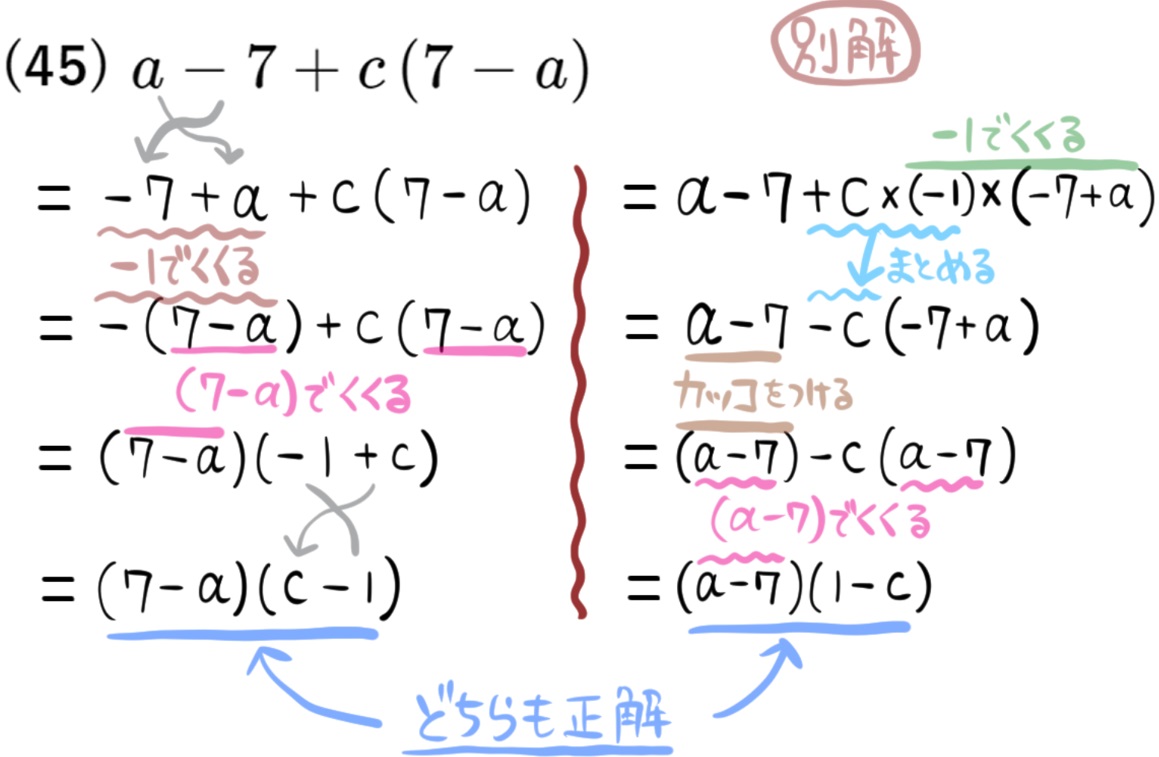
(45) \(a-7+c\left( 7-a\right) \)
別解のほうが操作が難しいですが、参考書の解説などで、このあたりの操作を省略して説明されていることがあります。なので、難関を目指す方は習得しておくといいでしょう。
共通因数で２回くくりだす操作のある因数分解の応用問題
にゃんこ
ここからは、共通因数でくくりだす操作が２回ある応用問題を練習します。
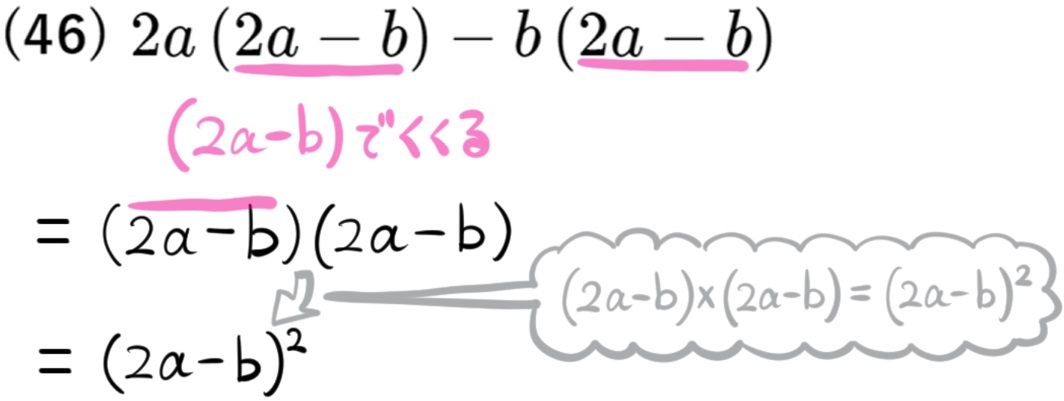
(50) \(\left( a+b\right) ^{2}\left( a-c\right) -\left( a+b\right) \left( a-c\right) ^{2}\)
さいごのこの問題は、文字におきかえてから式の形を観察すると、次の操作に気が付きやすいようになっています。この問題のように、おきかえる文字が２種類登場する場合は、おきかえずに考えようとすると次の変形に気が付きにくいでしょう。
にゃんこ
この50問をプリントアウトして学習したい方はこちら
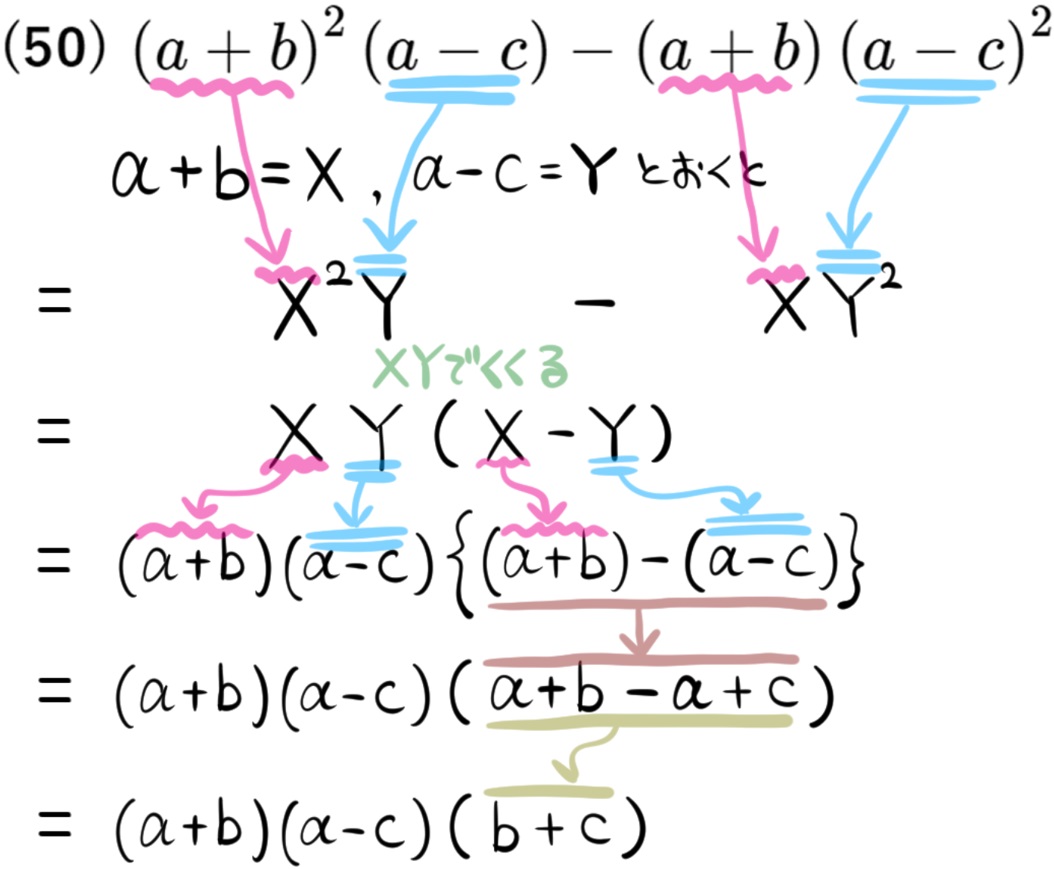
※この内容は特典として追加しています。
にゃんこ
次の３種をまとめてプリントアウトもできます
にゃんこ
３種のうち１種類だけをプリントアウトもOK
坂田先生
さらに縮小版も追加しました
中身紹介&説明ページはこちら
坂田先生
共通因数をくくりだす操作をすることによる因数分解の問題の練習は以上になります。
