

数Ⅰの出ない範囲や難易度まで勉強してしまうような、無駄なことをしたくないのです。

無駄な勉強時間を大幅にカットしてください。
- 高卒認定試験数学の出題範囲と難易度
- 高卒認定試験で使う中学数学の範囲
高卒認定試験数学の出題範囲を知るのと知らないとではこうも違う




- カッコをはずす工程のある一次不等式
- 小数のまざった一次不等式
- 分数の形が登場する一次不等式
- 連立不等式
















高卒認定試験数学の出題範囲と難易度

- 1:整式の加法減法
- 2:因数分解・展開・分母の有理化
- 3:集合と命題
- 4:一次不等式
- 5:二次関数
- 6:二次不等式
- 7:三角比
- 8:データの分析


式の計算と集合(加法減法・因数分解・展開・有理化・不等式)の範囲
因数分解はたすきがけを利用する内容が頻出となっています。
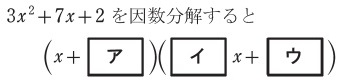
このような難易度の問題がベストでしょう。



市販の数学問題集(チャートなど)は、これ以外の範囲が掲載されていたり、これ以上の難易度のものが多数あります。
それらを使う場合は『過去問分析ページ』で紹介している過去問のパターンを見ながら、範囲をしぼって対策してください。
このパターン専用に作ったドリルは、次のような感じになります。
1:Aのみのパターン


(1)の解答

※有料版では、中学数学で使う部分だけ&過去問頻出テーマのすべての問題を動画解説しています。(ここにはない文章題の対策動画なども全収録)
2:ABCパターン
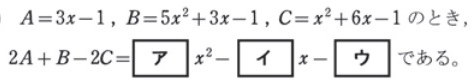

(1)の解答


このあたりの問題を対策しようとなると、先に中学数学の因数分解と展開(中3で学習します)の基本問題の復習をしておくと、スムーズに身に付きます。

(1)(4)の解答

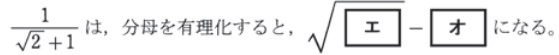

(1)(6)の解答

この分野をまず最初に学習すべきは、この問題になります。
この理解があるかどうかを聞いてくる問題が過去多数出題されています。
この問題&解答は無料で入手できますので、ぜひともプリントアウトして役立ててください。



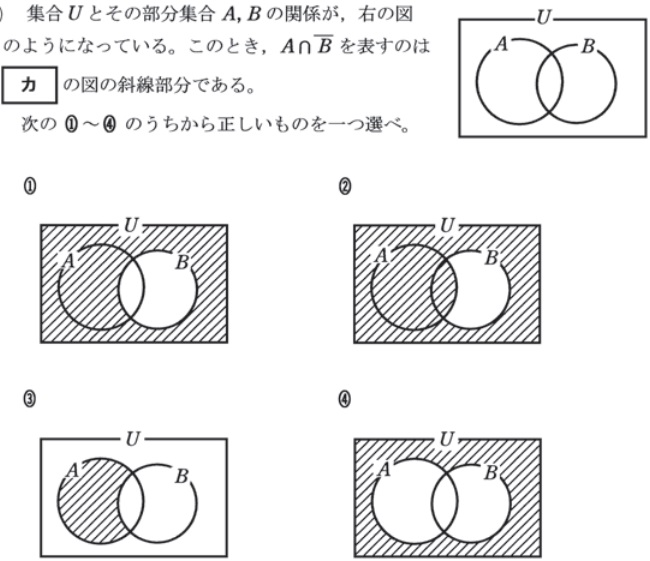
次に、集合図はこの分野かつこの難易度のものを練習します。

AかつB、AまたはB
について理解しているかどうかを問う問題です。

(1)の解答


冒頭で紹介した、かっこのある一次不等式です。無料で入手できます。



2:小数のある一次不等式


(1)(4)の解答

3:分数のある一次不等式


(1)(4)の解答

 けれども、文章問題そのものがバリエーションがありますので、対策をとりあえず後回しにすることをおすすめしています。
けれども、文章問題そのものがバリエーションがありますので、対策をとりあえず後回しにすることをおすすめしています。特に中学数学で、方程式の文章題が苦手だった場合は、時間がかかってしまう可能性があります。
個人的には費用対効果が小さい分野だと思っているので、これ以外を勉強したあとに、時間的余裕があればとりかかるようにしてください。
中学数学の方程式の文章題が苦手でなかった方以外はとにかく後回しにしましょう。
二次関数・二次不等式の出題範囲
この単元における出題範囲を一言で言えば、二次関数の式とグラフを理解していますか?というものです。
難易度的には教科書の基礎レベルのものがほとんどです。
しかし、中学数学の関数から復習される方は、一番対策に時間がかかってしまう可能性があります。
時間のない方は、次の三角比からとりかかるほうがいいかもしれません。

2:頂点の座標を求める力
この2点を対策します。
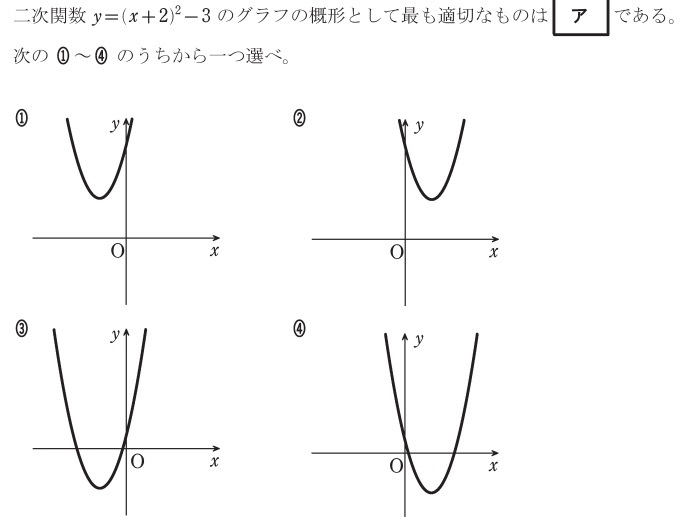




2:二次関数の定数を求める問題
3:頂点の座標と、そのグラフが通る座標で二次関数を作る問題
4:二次関数の式から頂点を求める問題
5:二次関数の最大値・最小値を求める問題
6:二次関数とx軸との共有点

1:グラフを移動させる問題


(1)(2)の解答

2:二次関数の定数を求める問題


(1)の解答

3:頂点の座標と、そのグラフが通る座標で二次関数を作る問題


(1)の解答

4:二次関数の式から頂点を求める問題
平方完成せずに、頂点の座標を簡単に求める手順を書いておきました。
平方完成ができる場合はそれで解いても大丈夫です。

(1)(4)の解答

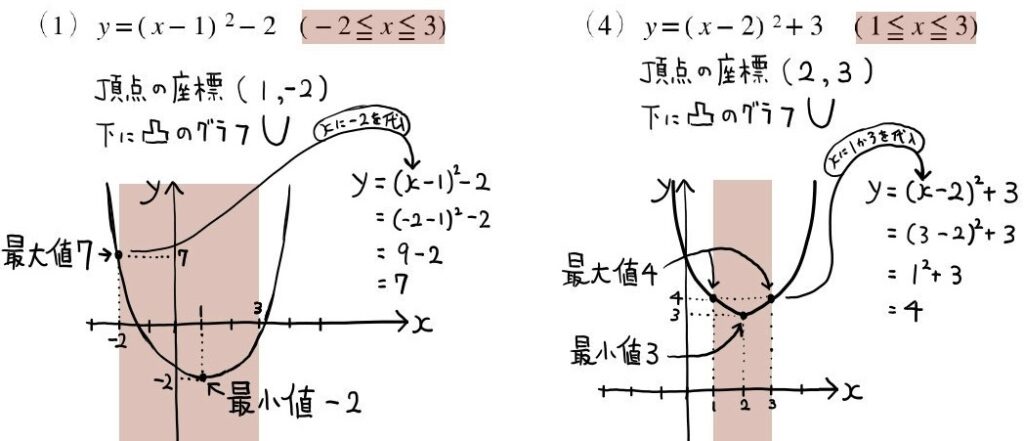
5:二次関数の最大値・最小値の問題

変域のある場合はこのようにグラフを書いて求めます。
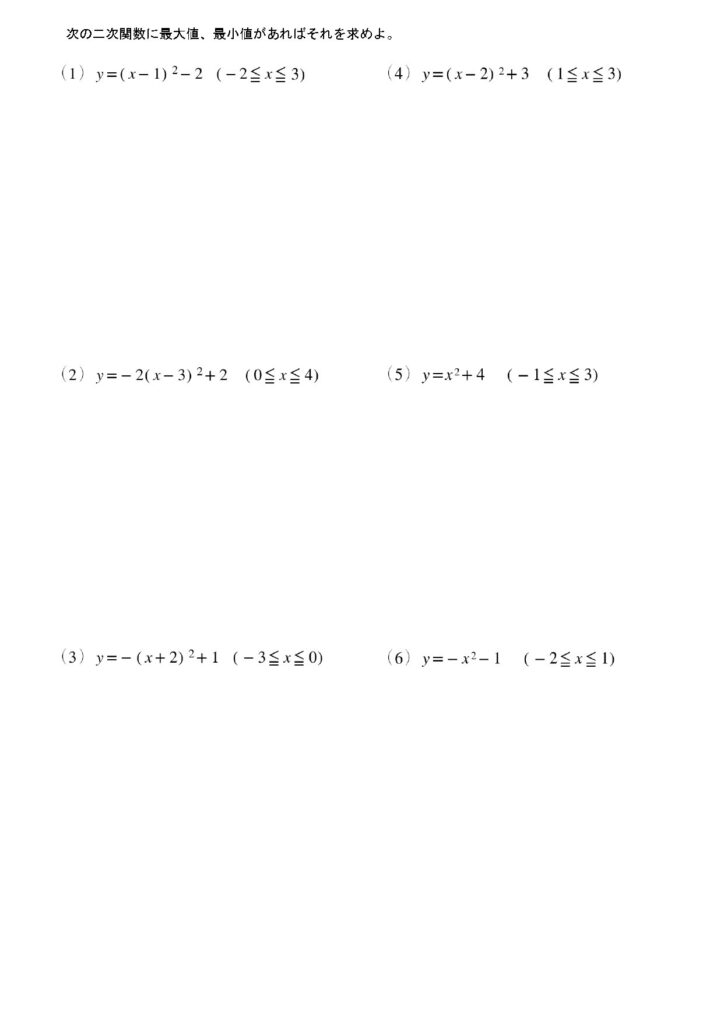
(1)(4)の解答
6:二次関数とx軸との共有点


(1)(5)の解答


2:二次不等式がx軸と1点で接する問題
3:二次不等式を解く問題

1:二次不等式がx軸と2点で交わる問題


(1)(2)の解答

2:二次不等式がx軸と1点で接する問題


(1)(2)(3)(4)の解答

3:二次不等式を解く問題


(1)(2)の解答

三角比の出題範囲

1:角度を求める練習問題
2:線分の長さを求める練習問題
3:sin cos tanの値を計算する問題
4:三角比の相互関係の公式を使った問題
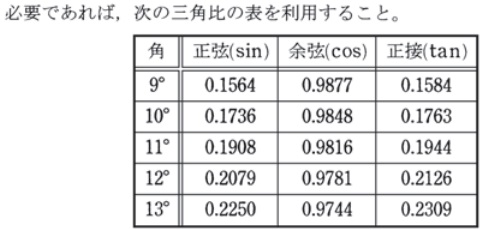
5:代表的な三角比の表を覚え、そこから計算する問題

1:角度を求める練習問題
この分野の最初のほうは、三角比を利用して角度や線分を求める範囲から出題されています。
この角度と線分の長さを求めるは対策までのコスパが良く、得点源としてほしいところです。
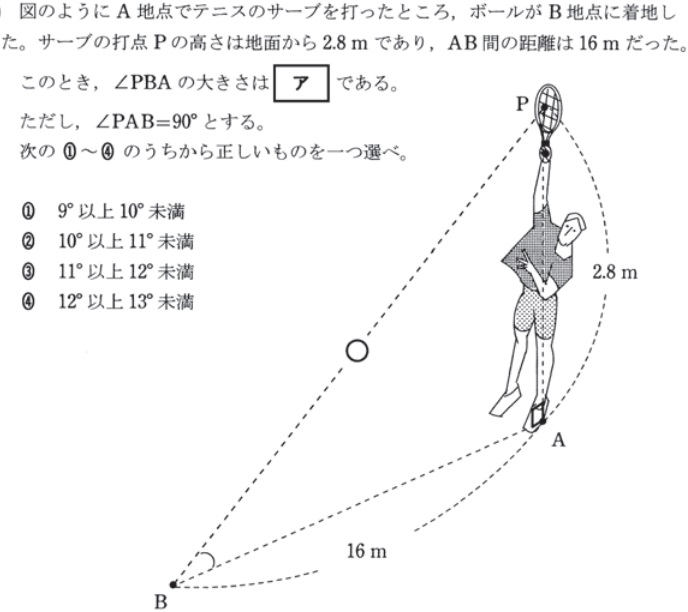
毎年イラストが付いていますが、三角形の問題としてとらえてください。
このような練習問題↓をしてから実際の過去問に慣れてください。



2:線分の長さを求める練習問題

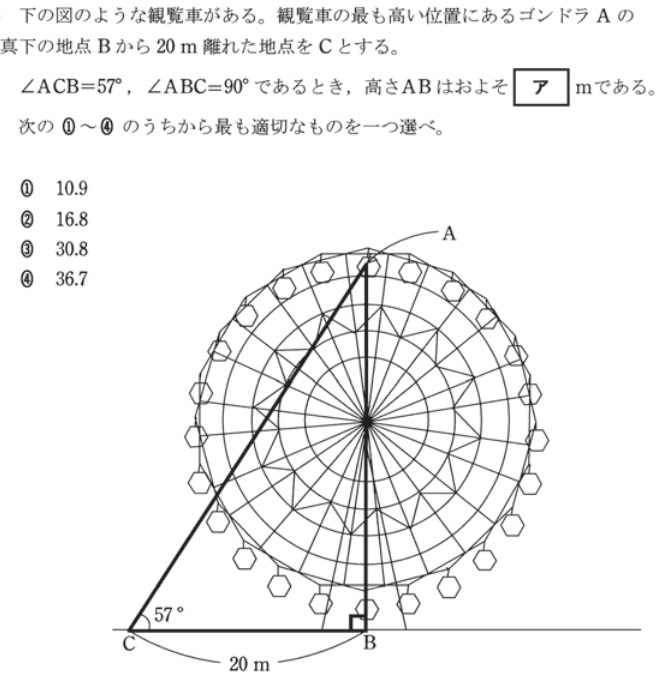

(1)(5)の解答

180°-θ、90°-θの三角比と式の値が出題されることがあります。
以下の公式を使って解きます。
・180−θの三角比の公式(0≦θ≦180)
sin(180−θ)=sinθ
cos(180−θ)=−cosθ
tan(180−θ)=−tanθ
・90−θの三角比の公式(0≦θ≦90)
sin(90−θ)=cosθ
cos(90−θ)=sinθ
このような練習問題に慣れておくといいでしょう。
3:sin cos tanの値を計算する問題



(1)(6)の解答

三角比の相互関係の公式を使った出題と、三角比の表から計算する問題が出ています。
4:三角比の相互関係の公式を使った問題


(1)の解答

5:代表的な三角比の表を覚え、そこから計算する問題
代表的な三角比を覚えて、それを利用して解答する問題が出題されています。

(1)(2)の解答

7:三角比を利用した面積の公式を使う問題
8:正弦定理の問題
ここはほぼ余弦定理を使う範囲なので、公式を暗記してひたすらあてはめて解答しましょう。
6:三角比の余弦定理の公式を使って解答する問題
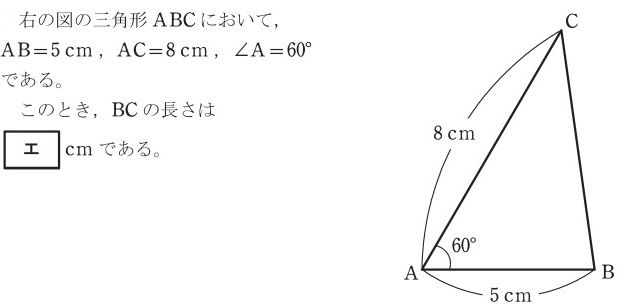

(1)の解答

7:三角比を利用した面積の公式を使う問題
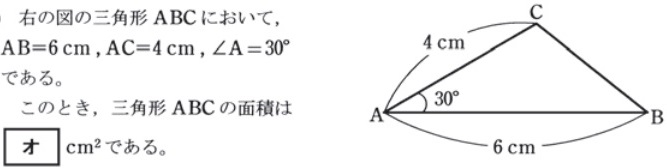
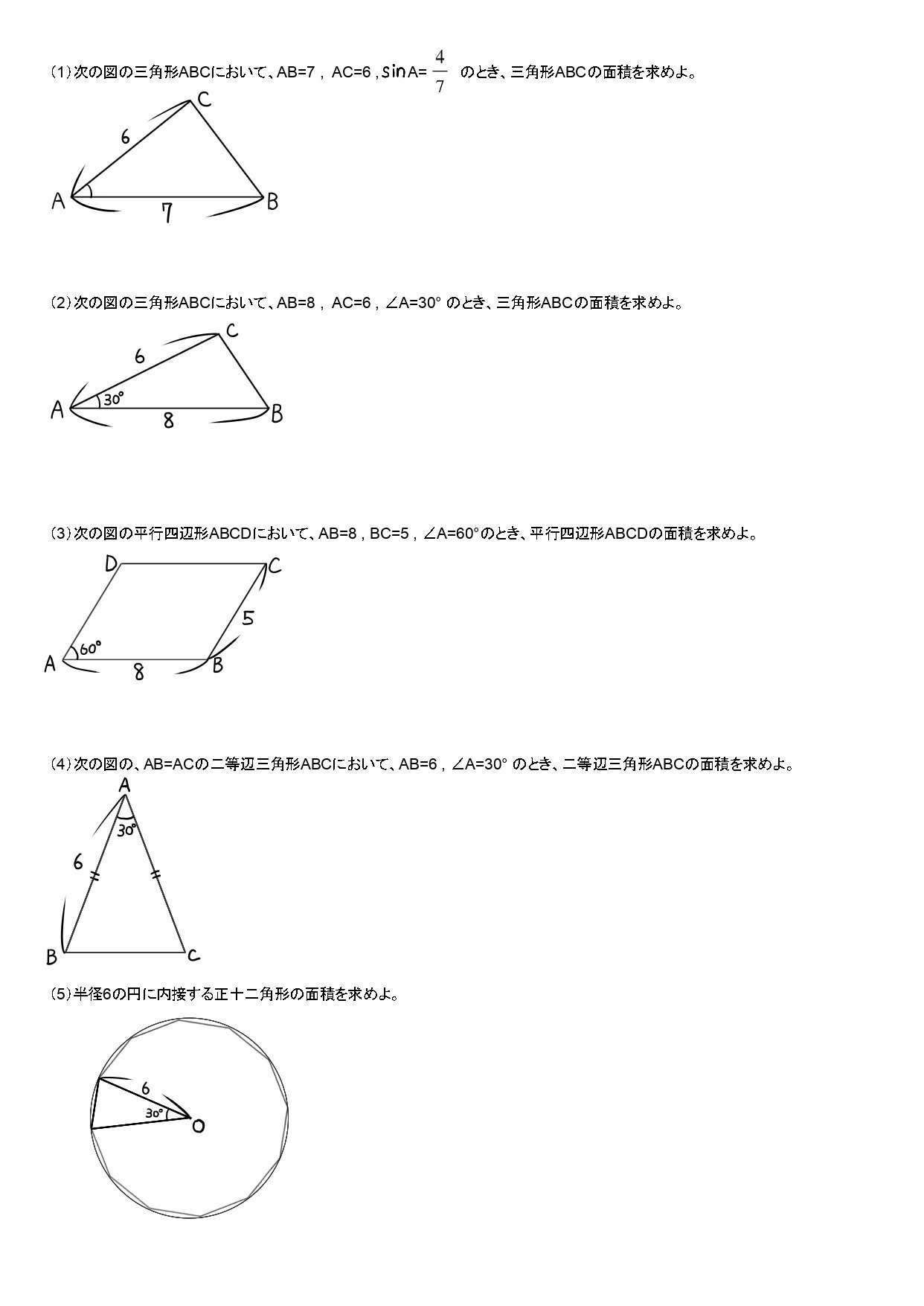
(1)の解答
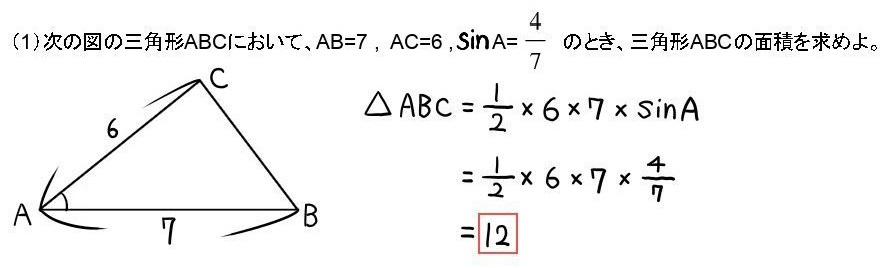
8:正弦定理の問題
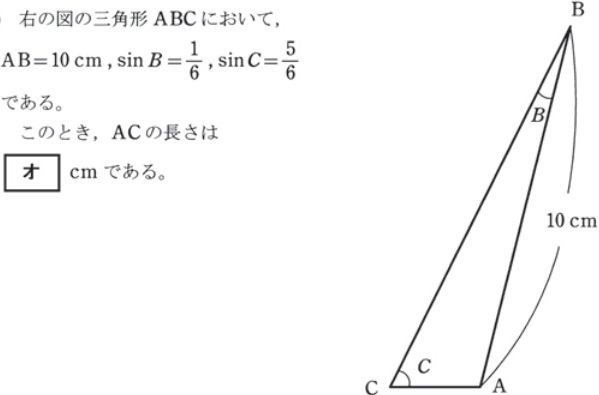

(1)の解答

データの分析の出題範囲

2:データから箱ひげ図を書く知識があるかをチェックする問題
3:箱ひげ図を読み取る問題
4:平均、分散、標準偏差の問題
5:相関係数の問題

1:データの分析の基本用語の問題

データの分析をする際の、基本的な各用語の意味を理解しているかを問う問題が出題されています。
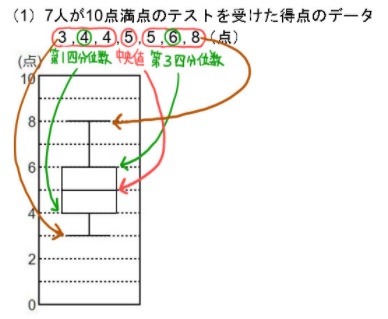
最大値、第3四分位数、中央値、第1四分位数、最小値、範囲、最頻値、平均値、についていくつかを取り上げた問題がよく出題されます。



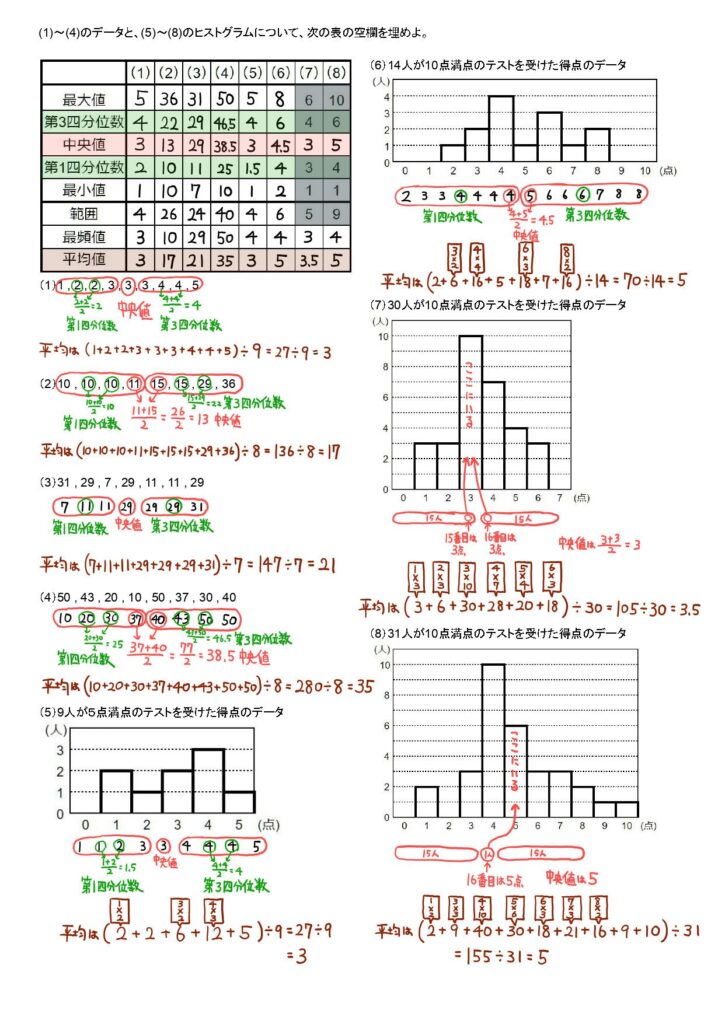
2:データから箱ひげ図を書く知識があるかをチェックする問題
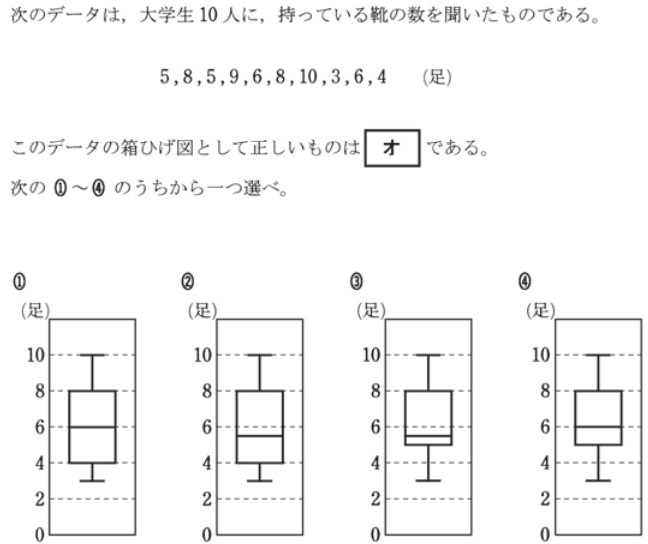

(1)の解答
3:箱ひげ図を読み取る問題
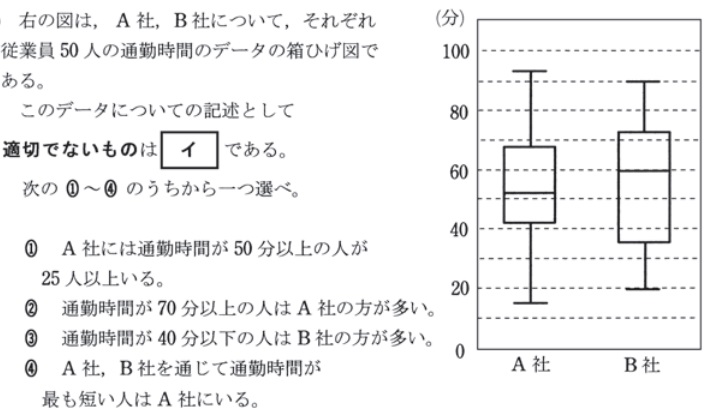
箱ひげ図の読み取りは、範囲と四分位範囲の違いをよく理解しておきましょう。範囲は最大値から最小値までの範囲で、四分位範囲は、第3四分位数から第1四分位数までの範囲です。

(1)の解答

4:平均値、分散、標準偏差を求める問題
 分散や平均を求める問題の頻度が高いです。分散や標準偏差を求める必要がある場合、公式は例年問題文に載っています。
分散や平均を求める問題の頻度が高いです。分散や標準偏差を求める必要がある場合、公式は例年問題文に載っています。ただ、分散をミスなく計算をするためには、次の問題の解き方にあるように、少し工夫して計算するほうがいいでしょう。

(1)(4)の解答
このように、分散を求める際は、表にして公式を計算していく練習をしてください。

5:相関係数の問題
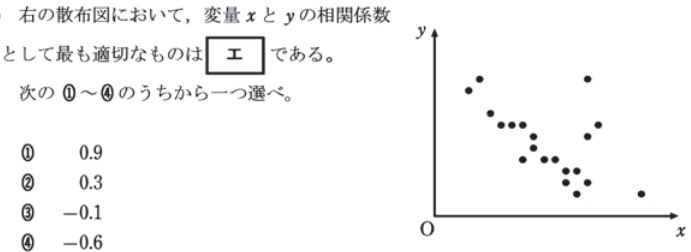 データから散布図を作成する力を問う問題と、相関係数についての理解を問う問題が出題されています。
データから散布図を作成する力を問う問題と、相関係数についての理解を問う問題が出題されています。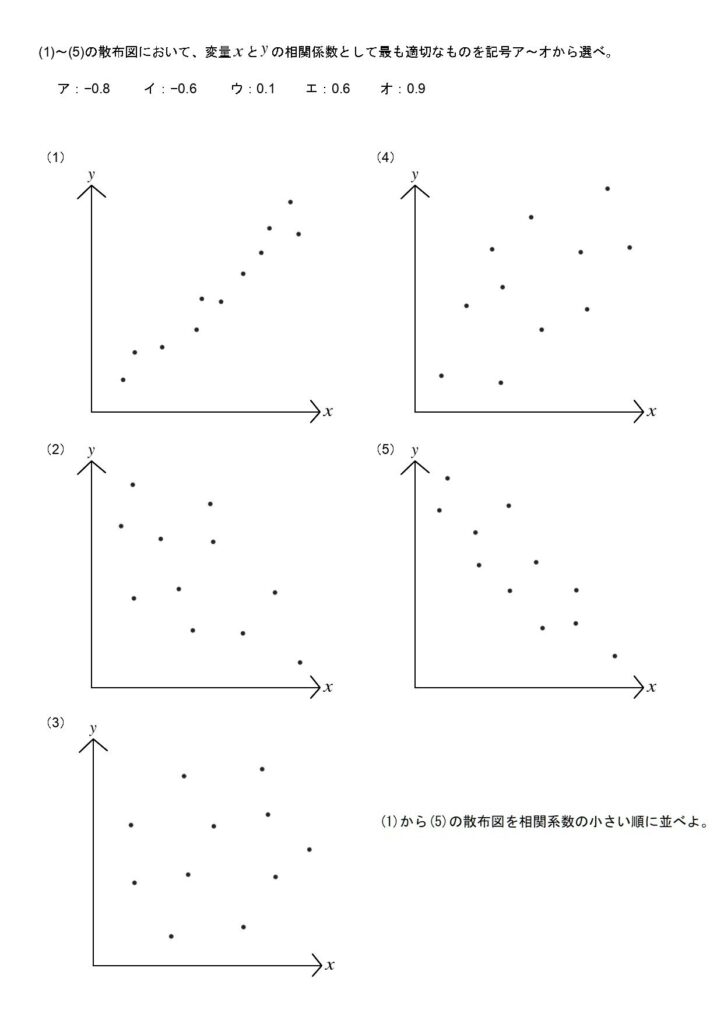
(1)(4)の解答

縦軸の要素が増加するにつれて、横軸の要素が増加する傾向が見られたときに、それは正の相関がある、と言えます。
逆に、縦軸の要素が減少するにつれて、横軸の要素が減少する傾向が見られたときに、それは負の相関がある、と言えます。
正の相関や負の相関を数値で表したものを相関係数と言います。
高卒認定試験で使う中学数学の範囲




- 中学1年2年3年生の計算問題(方程式も含む)
ただし、連立方程式はとりあえずとばしておいてください。高卒認定試験2の1で連立の一次不等式が出題される可能性がありますが、連立方程式を復習する必要があるとしたら、その場合にそなえてのことになります。
ただ、連立一次不等式は出題頻度が少ないので、とりあえずあとまわしにしてもいいです。2の1は、一次不等式のカッコ付きと、小数と分数の一次不等式が出題されますので、その対策をして時間的に余裕があった場合のみ対策してください。 - 中学3年生の二次方程式の解の公式
4の2の『2次関数とX軸との共有点』を求める際に使います。 - 中3の二次関数のグラフの最初だけ
中学数学で学習する二次関数のグラフは、頂点が原点を通るパターンのみです。深く学習する必要はなく、関数の式を見て、それが上に凸のグラフになるか、下に凸のグラフになるかということがわかればOKです。 - 中1の方程式の文章題(ただし優先順位は低い)
方程式の文章題は高卒認定試験2の2の『一次不等式の文章題』で使用します。ただし、文章題はバリエーションがあるので、他の問題パターンの対策ができてから余裕があればとりかかるようにしてください。
















































 本名:坂田健太(滋賀県)
本名:坂田健太(滋賀県)