にゃんこ
高卒認定試験の数学で因数分解のたすきがけが出題されていますが、その解き方をわかりやすく教えてください。
また、それ以外の高認数学の問題に関しても対策しておいたほうがいいのか知りたいです。
また、それ以外の高認数学の問題に関しても対策しておいたほうがいいのか知りたいです。
坂田先生
この質問にお答えします。
このページの内容
- 過去に高卒認定試験で出題された因数分解のたすきがけ問題の対策
- 高卒認定試験数学のその他の出題パターン
にゃんこ
【そもそも中学数学から苦手だった方へ】
１：高認数学で使う部分だけの中学数学
２：高認数学で使う部分だけの高校数学
３：過去問頻出パターン
この３つをマスターできる超ていねいな講座をリリースしました。
１：高認数学で使う部分だけの中学数学
２：高認数学で使う部分だけの高校数学
３：過去問頻出パターン
この３つをマスターできる超ていねいな講座をリリースしました。
・過去問頻出パターンを網羅したドリル(約50パターン)
・超ていねいな授業動画２６本(計10時間以上)
短い解説文にチンプンカンプンな方や、出ない範囲まで勉強したくない方は、最短コースで９割ゲットを目指してください☆
坂田先生
たっぷり無料版をこちらのぺージにて試してからご検討ください。
にゃんこ
プリンターがご自宅にない方はコンビニなどでのプリントアウトもご検討くださいm(__)m
過去に高卒認定試験で出題された因数分解のたすきがけ問題の対策
坂田先生
高卒認定試験の数学では、次のような「たすきがけを使って解く因数分解の問題」がよく出題されています。
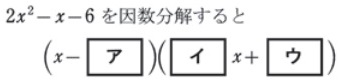
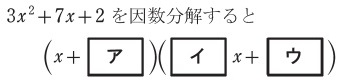
これって全部、数学Ⅰで学習する因数分解のたすきがけの解き方で解答できますので、その手順についてこれからご説明します。
たすきがけを使った因数分解の手順
高卒認定試験数学のその他の出題パターン
にゃんこ
高卒認定試験の数学で因数分解の解き方を覚えようとする場合、基本的には、先程説明したたすきがけの手順をマスターすれば、ほぼ対応できます。
坂田先生
ただし、高認数学では、たすきがけ以外の解法で解く問題も出題される可能性もゼロではありません。
このように高卒認定試験の数学（平成28年度）の問題を見ると、たすきがけではない解法を要求しています。
【置き換えによる因数分解の解き方】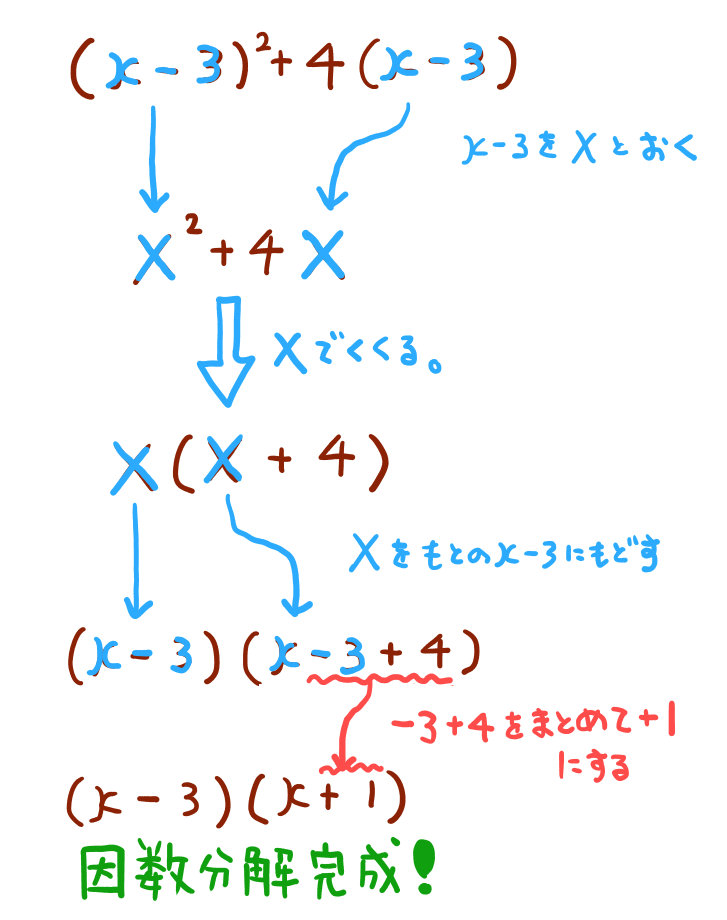
これ以外の解き方は近年見たことはありませんが、完璧に対応しておきたいという場合は、数Ⅰの因数分解の基本パターンを対応しておくといいでしょう。
ただし、コスパ的にあまりオススメはしません。出題される可能性が極めて低いからです。
坂田先生
この問題も実は中学３年生の因数分解の範囲です。
にゃんこ
過去問を分析するとわかりますが、因数分解の分野以外にも高確率で出題される問題パターンが数多くあります。
坂田先生
正直、頻出パターンの対応ができているだけで十分合格点は取ることが可能です。
そんな頻出パターンをすべて対策してから、余裕があれば取り組むという程度の優先順位でないと、必要な勉強時間がどんどんふくらんでしまいます。
高卒認定試験は、科目数が多いので、『過去問を分析して必要なパターンだけ対策する』ということを最重要に取り組んでください。
坂田先生
にゃんこ
という方のために、無料部分たっぷりの講座をこちらに用意しました。
にゃんこ
高認数学講座たっぷり無料版をただ今プレゼント中★
詳細ページ：たっぷり無料版(失敗しない勉強方法解説付き)
坂田先生
中学数学の基礎から高認数学過去問レベルまで対策できる講座です。
本名：坂田健太（滋賀県）
参考：たすきがけのやり方｜因数分解の練習問題付きで応用までわかりやすく解説
※ただし、後半の応用問題の部分は必要ありませんのでスルーしてください。
この動画では、たすきがけの手順とどうして解き方でOKになるのか、という理屈の部分をちゃんと説明しようとしています。
ただ、理屈は理解できなくても、方法を覚えてマネさえすればちゃんと解けますので、そこまでこだわらないくても大丈夫です。
まずこの動画を見る際に、前提として知っておいてほしいのが、展開と因数分解は逆の計算手順だということです。
(2x＋5)(3x＋4)というのは、(2x＋5)のかたまり掛ける(3x＋4)のかたまり、というように掛け算でつながった状態になっていますね。
このように、掛け算でつながった状態のことを因数分解されたかたちだと思っておいてください。
最初に展開の話から説明をはじめていますが、展開とは、因数分解されたかたちの式をバラバラにする手順、だと思っておいてください。