にゃんこ
高卒認定試験の数学は、過去問を分析するとかなりの頻出パターンがあるのを知っていましたか？
坂田先生
数Ⅰの参考書などで闇雲に解き散らかすよりも、まずはこのページを読んで、過去問の傾向を知ってから、コスパの良い対策をしてください。数Ⅰ全部を学習するなんてことは本当にやめてください。それだと仕上げるのに何ヶ月かかるかわかりません。
にゃんこ
ここでは、高卒認定試験数学の過去問をプロ講師が研究し、出題傾向を分析した結果を公開しています。活用してください。
にゃんこ
【そもそも中学数学から苦手だった方へ】
１：高認数学で使う部分だけの中学数学
２：高認数学で使う部分だけの高校数学
３：過去問頻出パターン
この３つをマスターできる超ていねいな講座をリリースしました。
１：高認数学で使う部分だけの中学数学
２：高認数学で使う部分だけの高校数学
３：過去問頻出パターン
この３つをマスターできる超ていねいな講座をリリースしました。
・過去問頻出パターンを網羅したドリル(約50パターン)
・超ていねいな授業動画２６本(計10時間以上)
短い解説文にチンプンカンプンな方や、出ない範囲まで勉強したくない方は、最短コースで９割ゲットを目指してください☆
坂田先生
たっぷり無料版をこちらのぺージにて試してからご検討ください。
にゃんこ
プリンターがご自宅にない方はコンビニなどでのプリントアウトもご検討くださいm(__)m
高卒認定試験の数学過去問を出題パターン別に解説&対策
因数分解、整式の加法減法の過去問パターン
にゃんこ
因数分解と文字式の問題が主な出題内容です。過去問の傾向を見ると、高卒認定試験の因数分解はたすきがけが、今のところほとんどです。
過去問頻出パターン：たすきがけを利用した因数分解
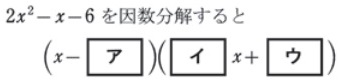
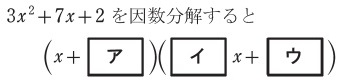
過去問頻出パターン：整式の加法減法
- Aのみのパターン
平成27年 
平成28年 
平成30年 
対策問題 
(1)の解答 
※有料講座では、中学数学で使う部分だけ&過去問頻出テーマのすべての問題を動画解説しています。（ここにはない文章題の対策動画なども全収録）
- ABCが登場するパターン
平成30年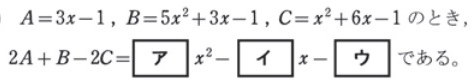 
平成29年 
対策問題 
(1)の解答 
式の展開、ルートの問題（分母の有理化）の過去問パターン
坂田先生
式の展開と、平方根のついた分母の有理化が主な出題内容です。
過去問頻出パターン：式の展開３項×３項
『式の展開』の単元は、３項×３項のパターンが多いです。もちろん、この形式以外も出る可能性はありますが、僕だったらここをまずマスターします。
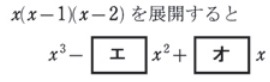
過去問頻出パターン：ルートの問題（分母の有理化）
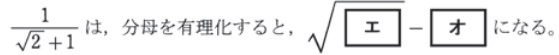
にゃんこ
もっと丁寧に解説するとこんな感じです☆
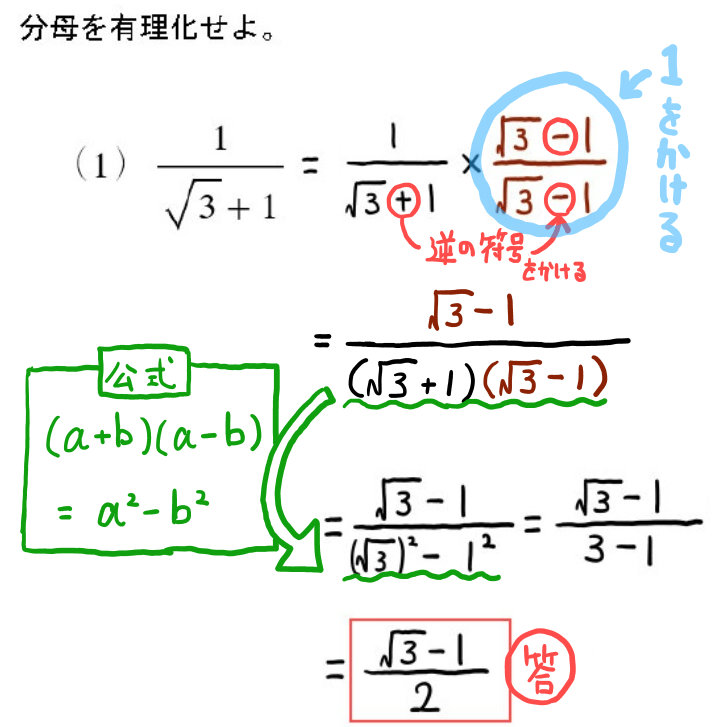
平方根のある分数式の計算
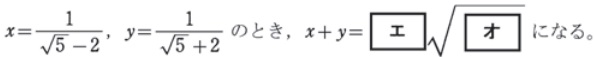
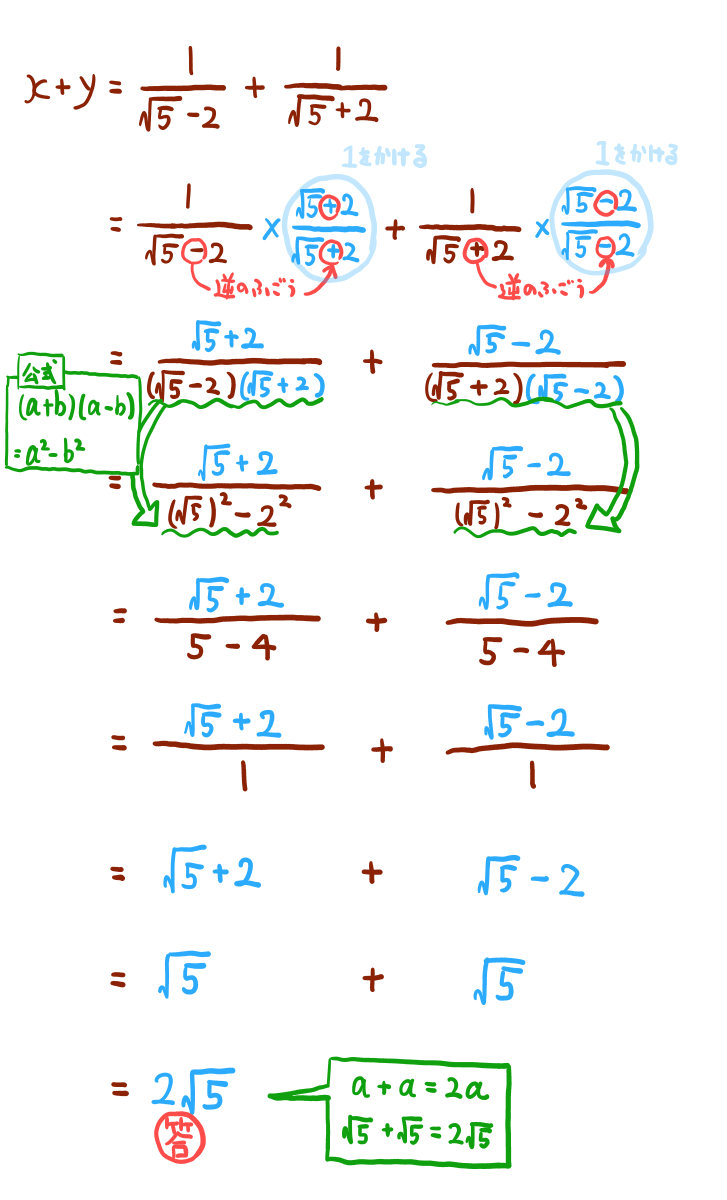
集合と必要条件・十分条件の判定の過去問パターン
坂田先生
集合の問題と必要条件・十分条件の判定問題が出題されています。
過去問頻出パターン：集合図と必要条件、十分条件
- 集合図の基本（余事象の範囲）
平成27年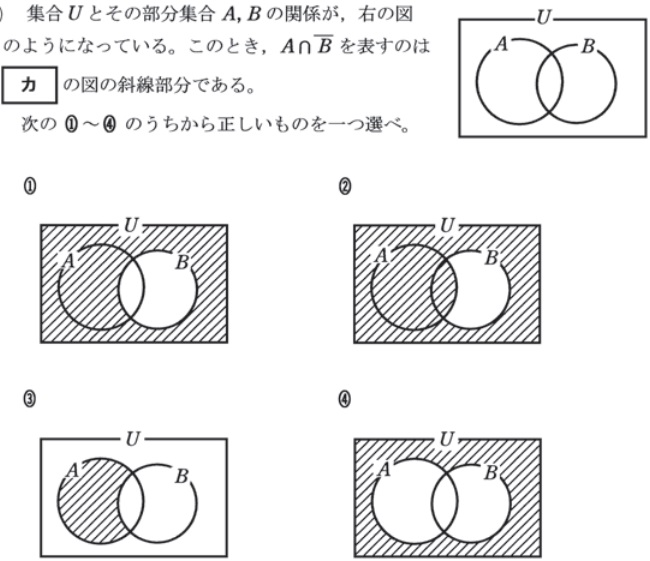 
- 共通部分（ＡかつＢ）と和集合（ＡまたはＢ）
平成27年 
平成29年 
平成30年 
令和1年 
対策問題 
(1)の解答 
過去問頻出パターン：必要条件、十分条件の判定問題
必要条件・十分条件の判定には、命題の真偽について確かめる必要がありますが、最初の理解がややとっつきにくい分野なので、わかりにくい場合はあとまわしにすることをおすすめします。
一次不等式（カッコ付き、小数、分数）の過去問パターン
にゃんこ
一次不等式を解く問題です。カッコをはずす不等式と、小数や分数のまざった不等式、それに連立不等式があります。
過去問頻出パターン：カッコ付き
過去問頻出パターン：小数
過去問頻出パターン：分数
連立一次不等式
坂田先生
このような連立一次不等式は出題頻度が少ないので、上の３つを対策してからとりかかってください。
一次不等式の文章問題の過去問パターン
一次不等式の文章問題
令和元年
平成30年
平成29年
平成27年
坂田先生
一次不等式の文章問題は、一見すると、ワンパターンな出題形式のように見えます。しかし、不等式を作る問題は内容にバリエーションがあり、対策にとても時間がかかってしまう可能性があります。
にゃんこ
中学数学で文章問題から方程式を作ることになれていない場合は、コスパが悪い問題となるかもしれません。少し解いてみて、難しいと感じた場合は、対策をあとまわしにすることをオススメします。
二次関数の式とグラフを対応させて理解しているかの過去問パターン
にゃんこ
二次関数の式とグラフを対応させて理解しているかという問題です。
過去問頻出パターン：二次関数のグラフ概形
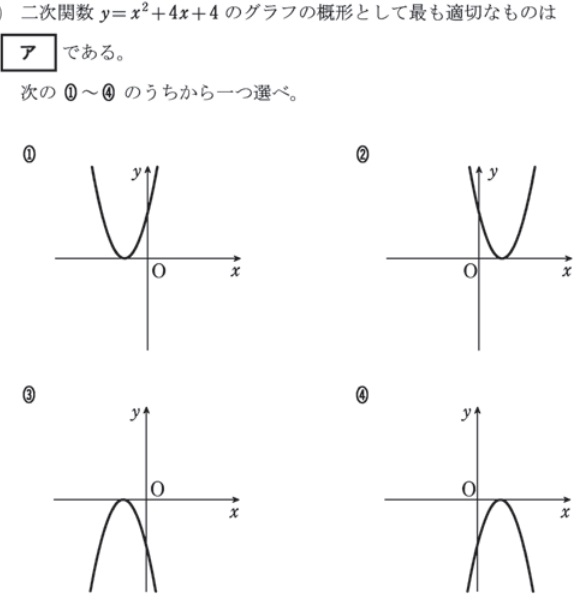
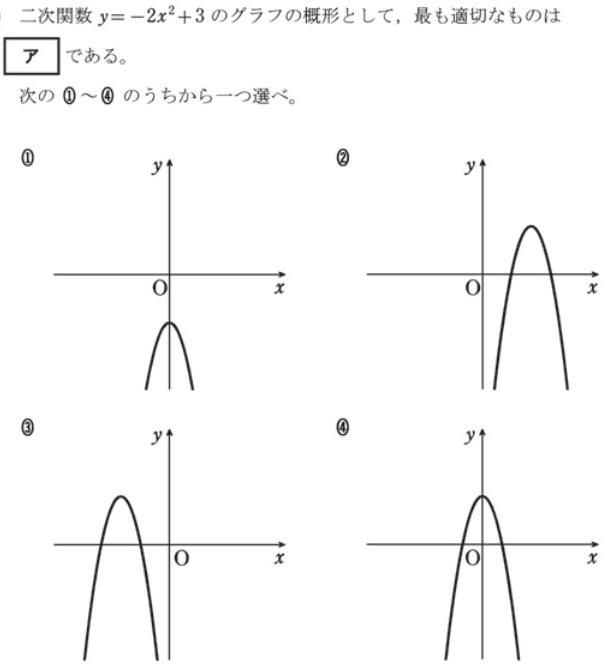
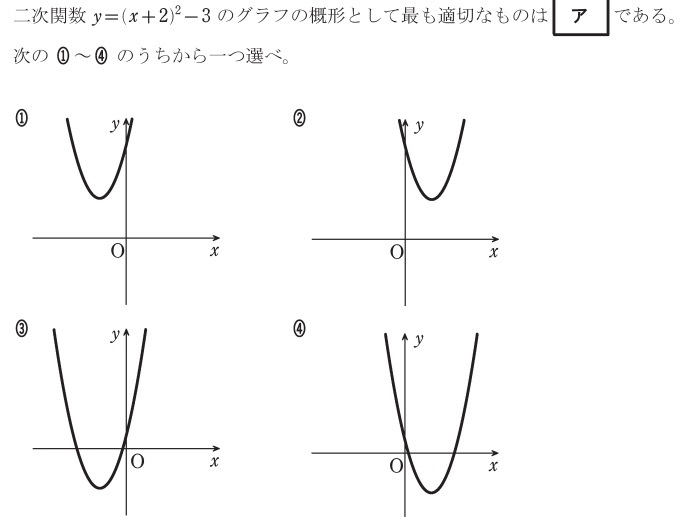
過去問頻出パターン：二次関数基礎グラフの平行移動後の関数
二次関数内の文字符号
二次関数内の文字の符号についての問題です。もちろん対策しておいたほうがいいですが、出題頻度は少ないので、優先順位としては弱いです。
定数を求める問題、頂点と通過する一点から二次関数を求める問題
にゃんこ
もうひとつは、頂点の座標と、そのグラフが通過する一点の座標から、二次関数の式を求める問題です。
過去問頻出パターン：定数を求める二次関数の問題
過去問頻出パターン：頂点と通過する一点
二次関数の一般形から頂点の座標を求める過去問パターン
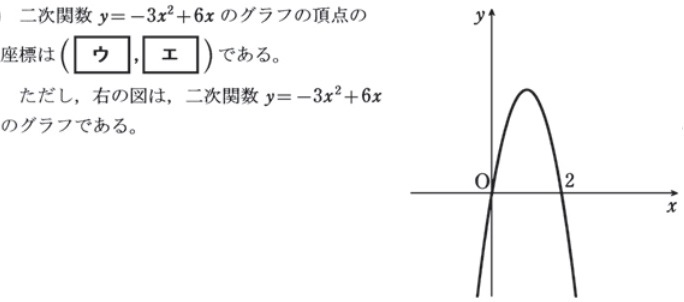
二次関数の一般形から頂点の座標を求める
平成30年
平成29年
平成28年
平成27年
坂田先生
二次関数の一般形から頂点の座標を求める問題です。平方完成させて頂点を求める方法もありますが、ややこしいという方のために、ここでは簡単な方法で解答しています。
二次関数の最大値・最小値の過去問パターン
にゃんこ
二次関数の最大値・最小値についての問題です。
過去問頻出パターン：二次関数の最大値・最小値
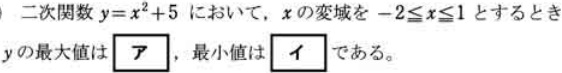
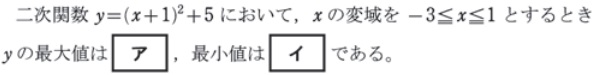
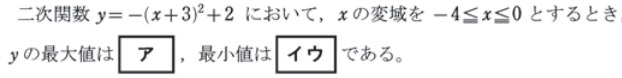
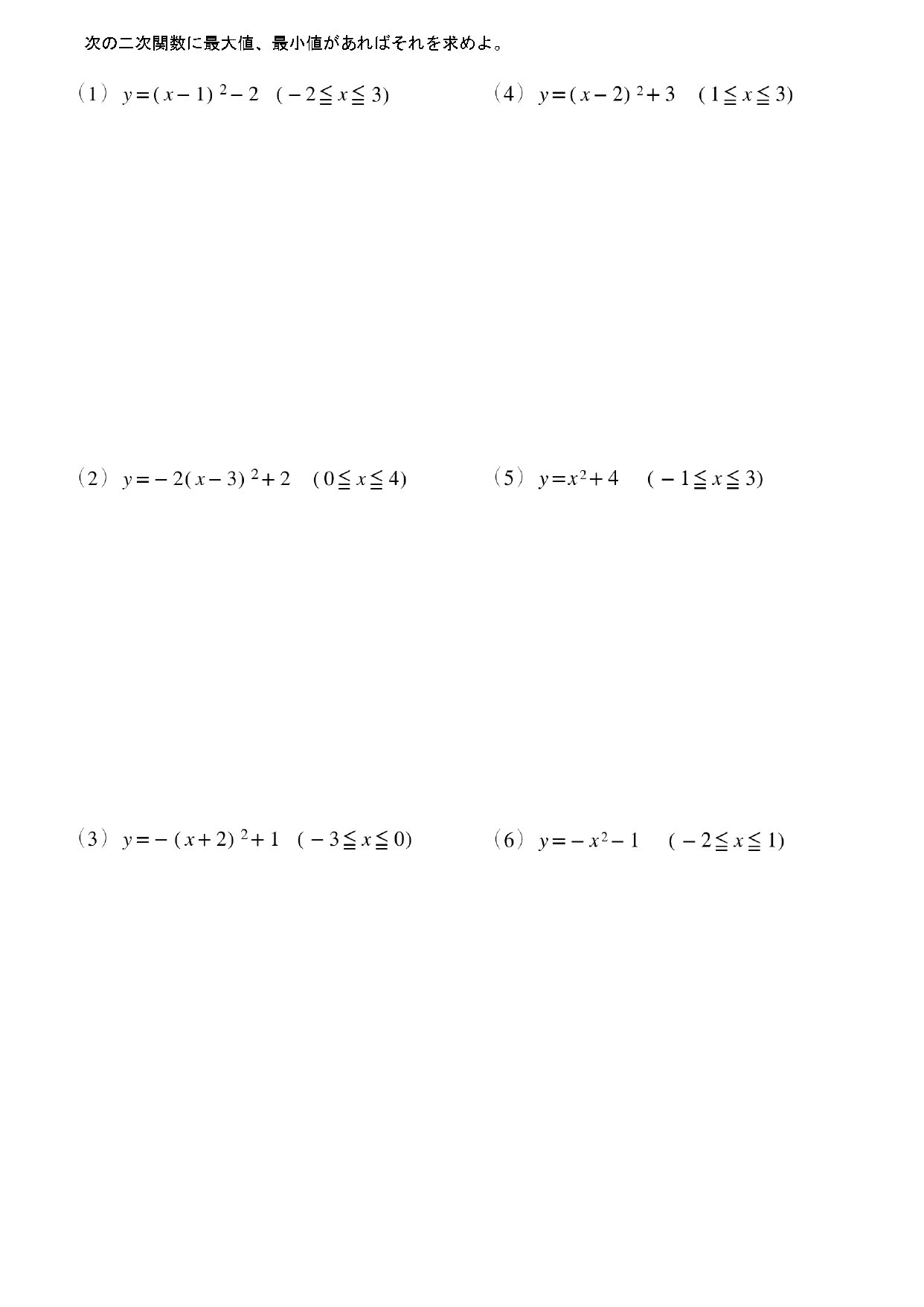
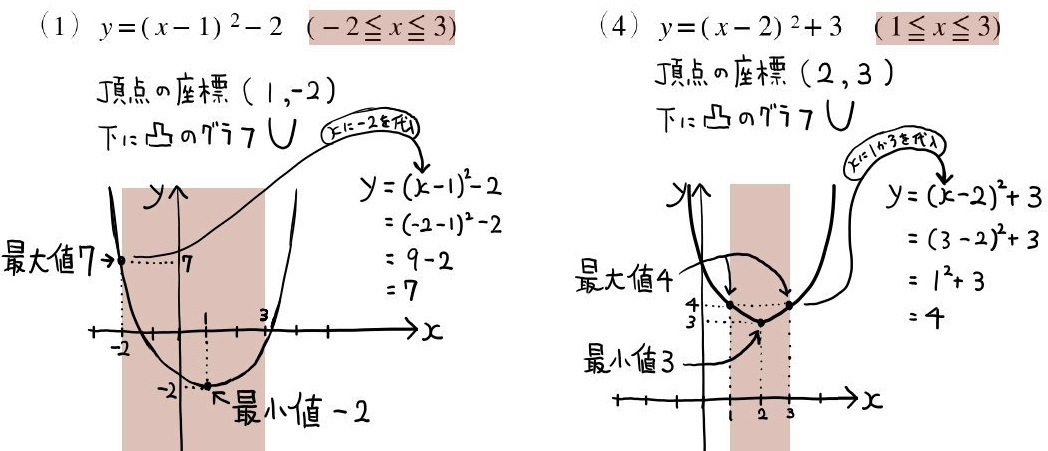
二次関数の最大値・最小値その２
二次関数のグラフとｘ軸との共有点の過去問パターン
二次関数のグラフとｘ軸との共有点
坂田先生
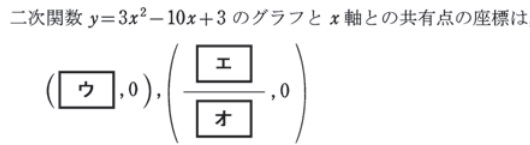
二次関数のグラフとｘ軸との共有点の問題です。座標を求める問題がほとんどですが、まれに共有点の個数を問う形式もあります。
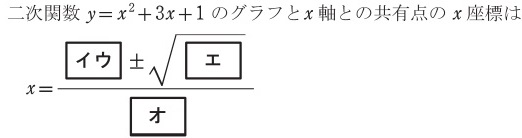
平成30年
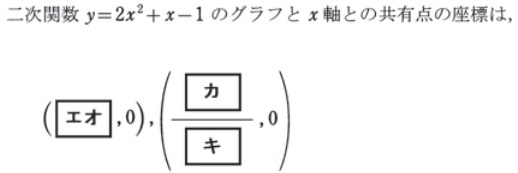
平成29年
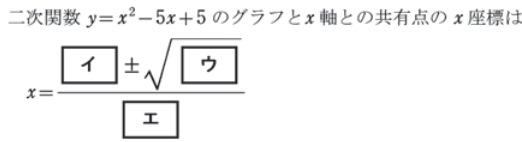
平成28年
二次不等式の解の過去問パターン
にゃんこ
二次不等式の解を求める問題です。高卒認定試験の数学では、グラフが最初から示されている出題形式と、グラフのない出題形式があります。
過去問頻出パターン：二次不等式グラフあり
- ２点で交わる二次不等式
平成28年 
平成29年 
平成30年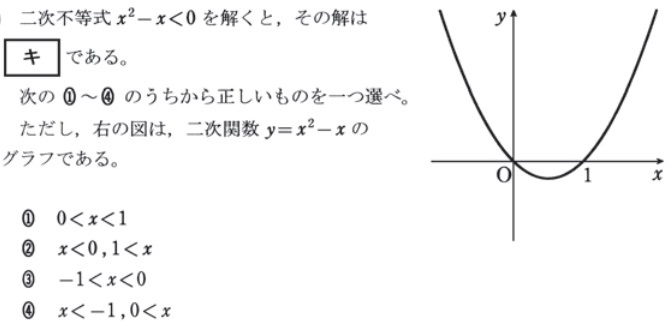 
対策問題 
(1)(2)の解答 
- ｘ軸に１点で接する二次不等式
令和1年 
平成28年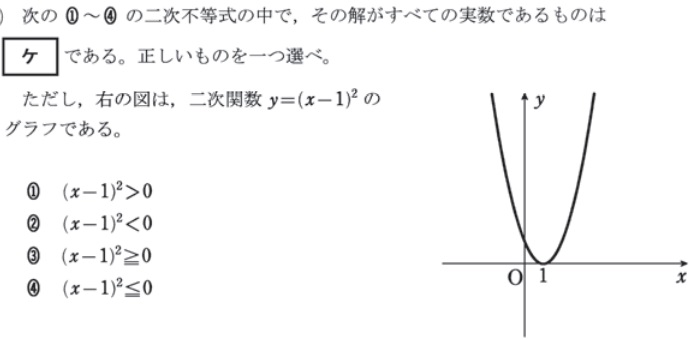 
対策問題 
(1)(2)(3)(4)の解答 
過去問頻出パターン：二次不等式を解く
三角比を利用して角度や線分を求める過去問パターン
坂田先生
三角比を利用して角度と線分を求める問題です。対策問題で基本的な計算を練習してから、文章やイラストで出題されても同様の手順で解いていけるよう最終確認をしてください。
三角比を利用して角度と線分を求める問題
つづいて、三角比を利用して角度や線分を求める問題です。
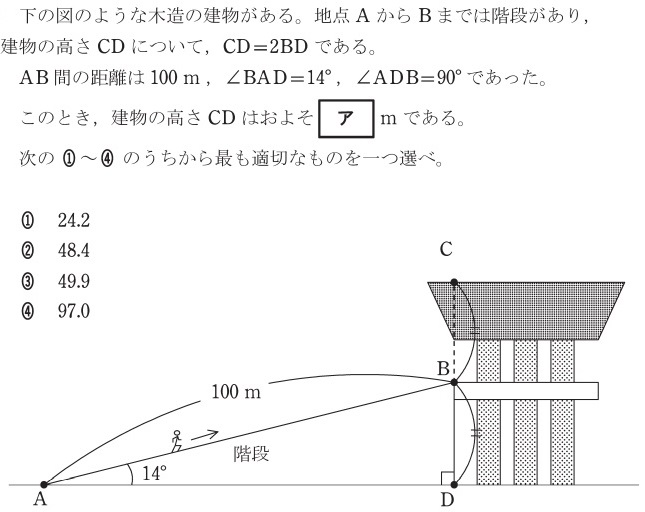
- 三角比を利用して角度を求める問題
令和元年
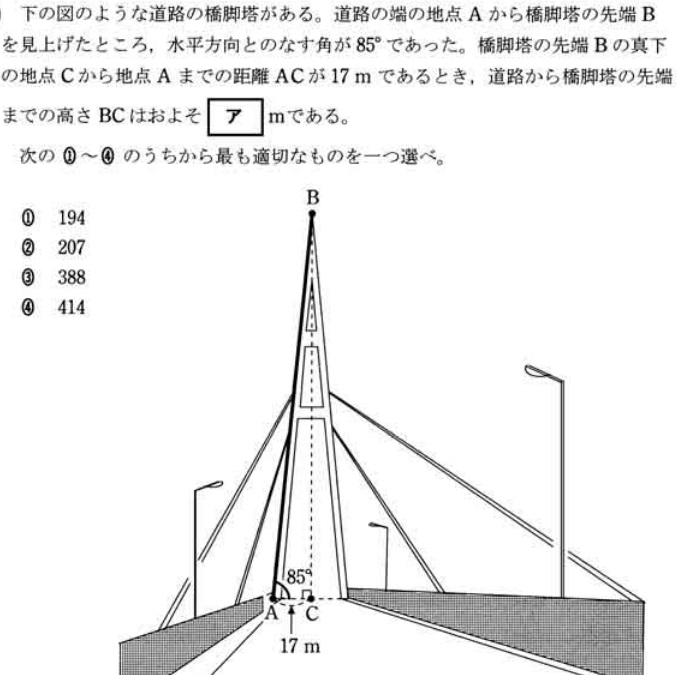
- 三角比を利用して線分を求める問題
平成27年
三角比の値を求める計算（180°－θ、90°－θ）の過去問パターン
公式180°－θ、90°－θを利用して求める問題
令和元年
平成30年
坂田先生
公式180°－θ、90°－θを利用して、三角比の値を求める計算の問題です。正直ここはかなりコスパがいいので、優先的に取り組んでほしいと思います。
三角比の相互関係の公式、三角比の表から計算する過去問パターン
三角比の相互関係の公式を使う問題
令和元年
平成29年
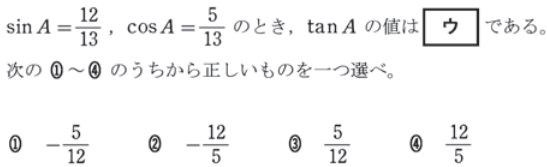
平成27年
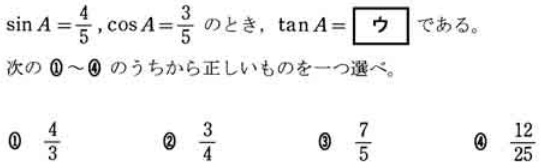
三角比の表から計算して求める問題
にゃんこ
30度や60度などの代表的な三角比の値を覚えて、それを使用して解くパターンの問題です。まずは対策問題で三角比の表を埋められるようにしてください。
平成28年
平成27年
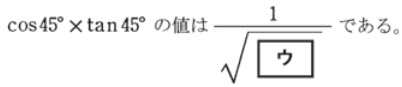
余弦定理
余弦定理
坂田先生
余弦定理の公式をただひたすら当てはめるだけの問題です。学習コスパ抜群です。
令和元年
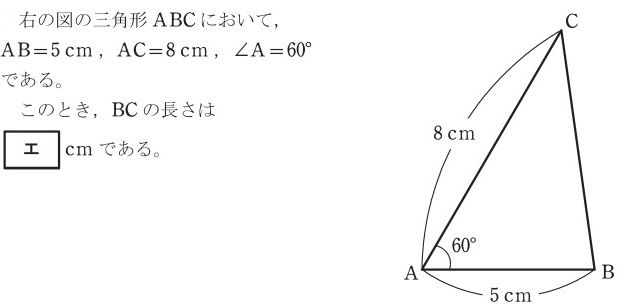
平成30年
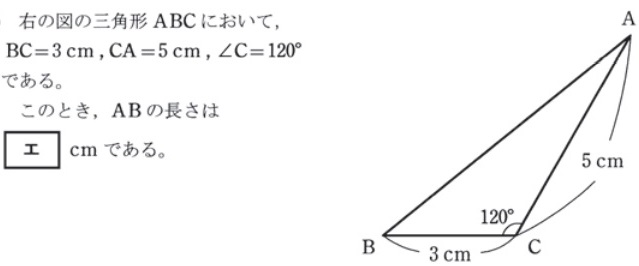
面積を求める公式、正弦定理の過去問パターン
坂田先生
ここもまた、面積を求める公式と正弦定理の公式を使うだけの問題です。解法はシンプルですが、計算ミスをしないよう、練習はかかさずしてください。
面積を求める公式
平成30年
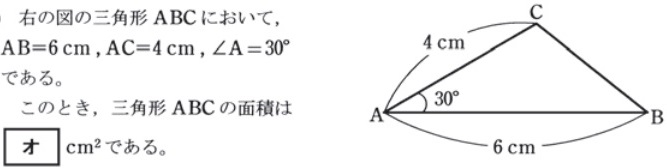
平成29年
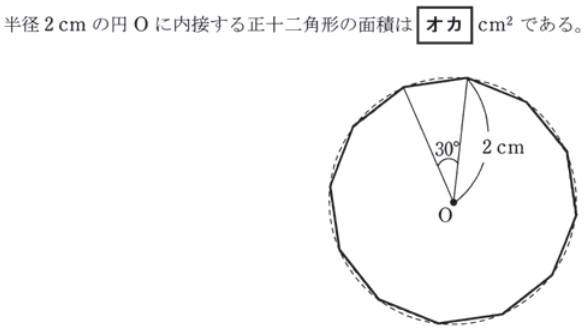
平成28年
平成27年
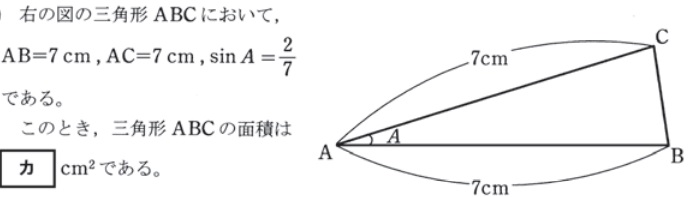
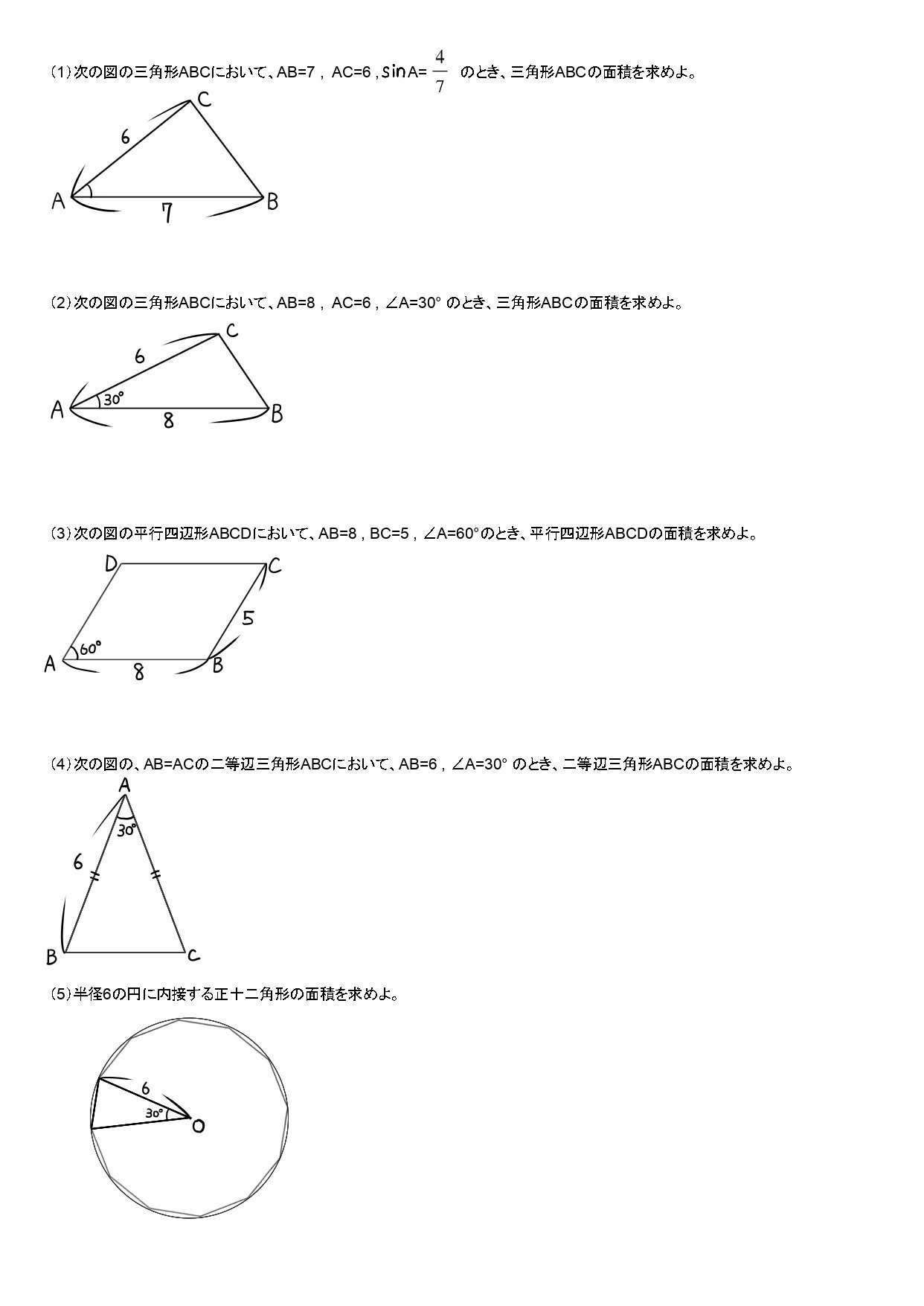
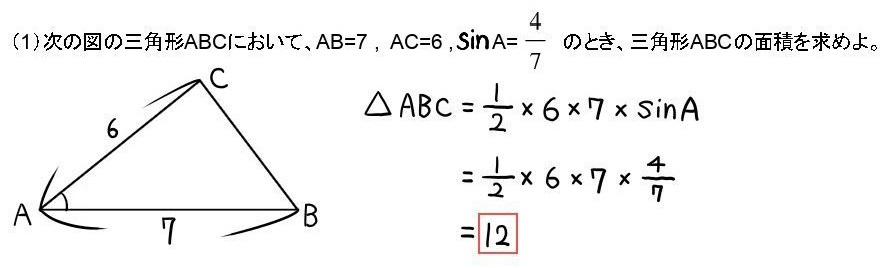
正弦定理
令和元年
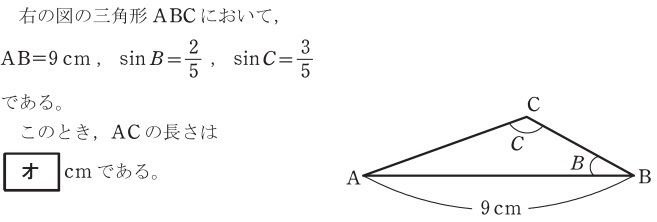
平成30年
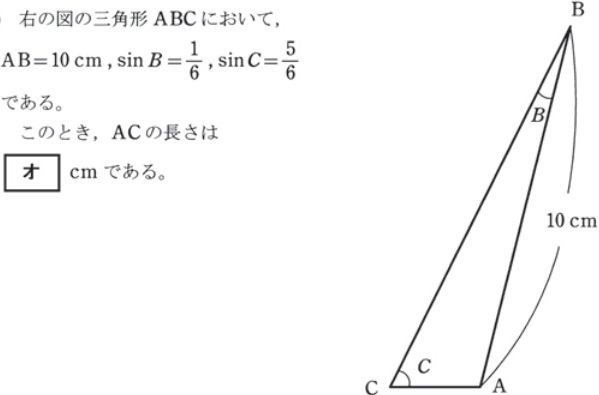
平成29年
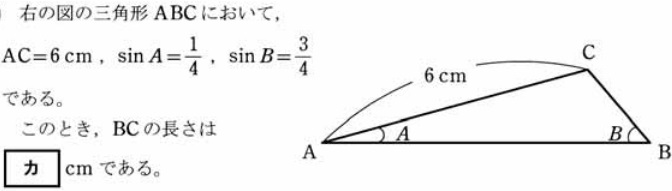
平成28年
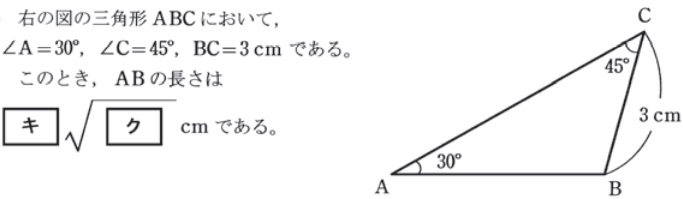
平成27年
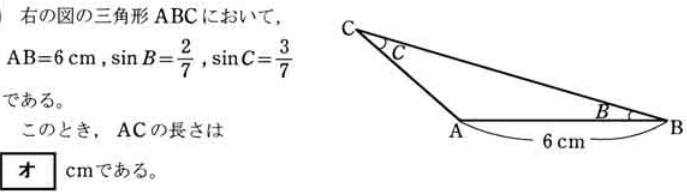
データの分析｜各用語の意味の過去問パターン
データの分析：各用語の意味
にゃんこ
データの分析において、各用語の意味（最大値、第３四分位数、中央値、第１四分位数、最小値、範囲、最頻値、平均値）についての理解を確認する問題です。
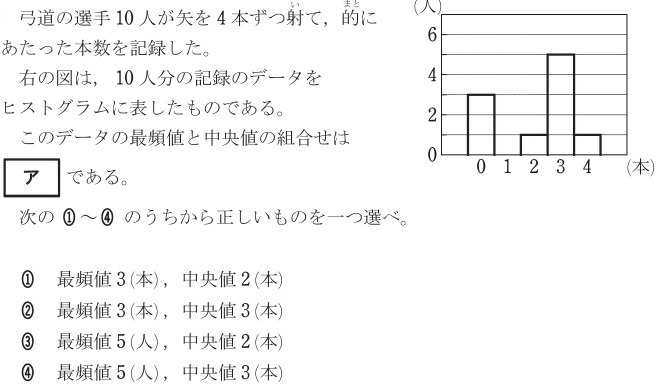
平成30年
平成29年
平成28年
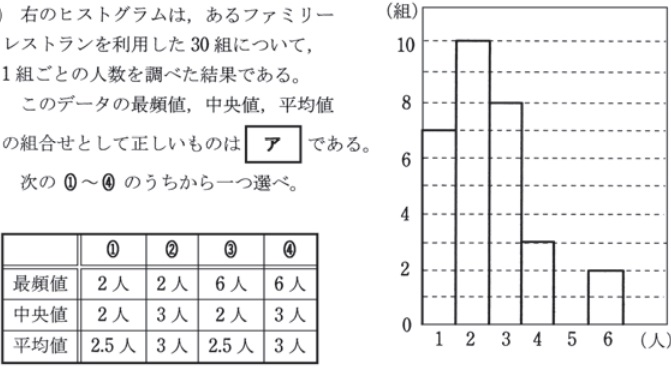
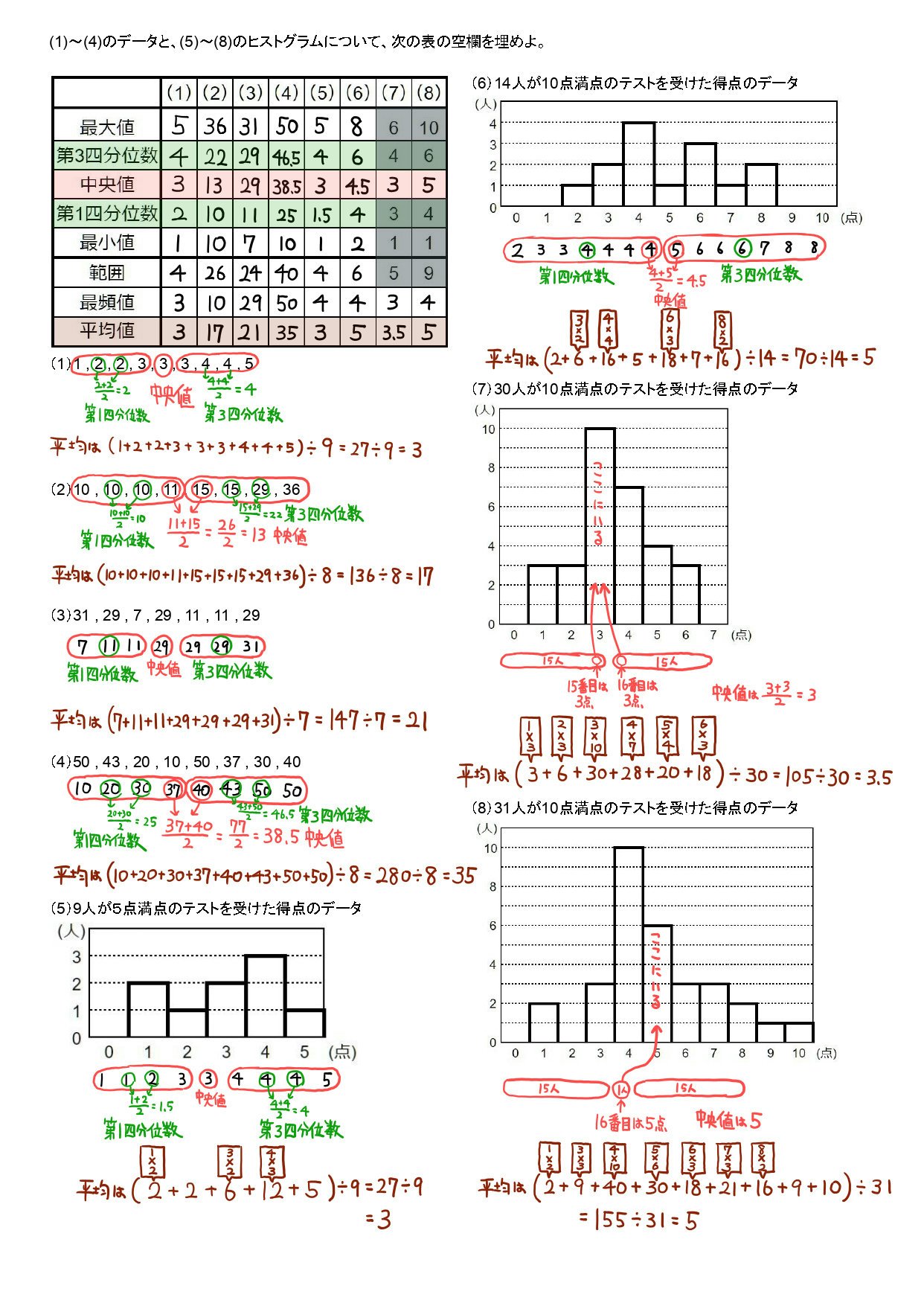
箱ひげ図を書く力を問う問題、読み取る問題の過去問パターン
坂田先生
過去問では、箱ひげ図のデータの特徴を読み取る問題と、箱ひげ図を書く力をチェックしている問題が頻出です。
箱ひげ図を書く力を問う問題
平成30年
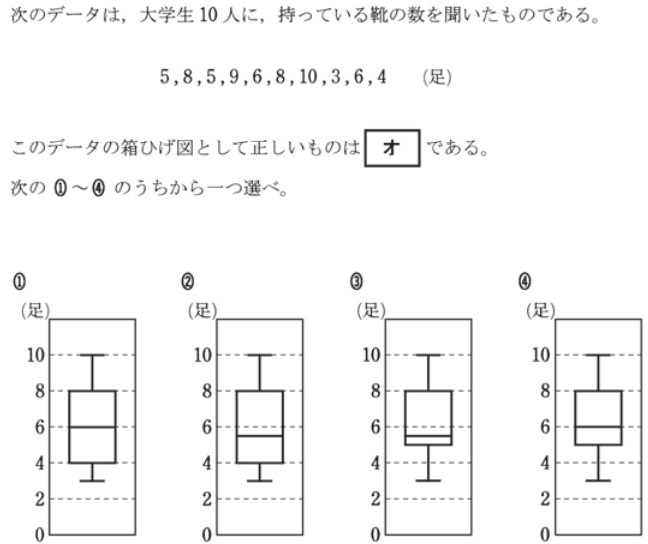
平成29年
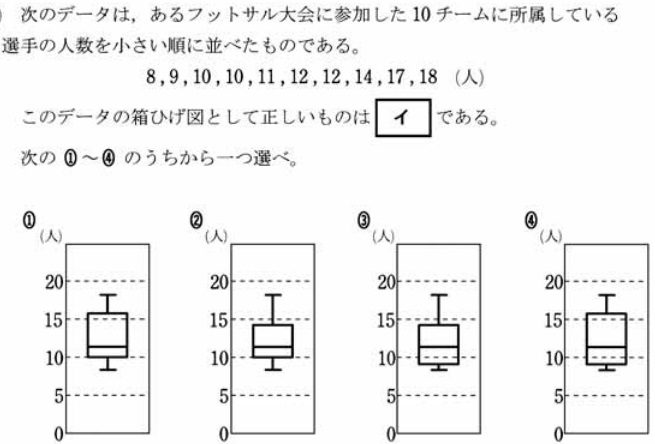
平成27年
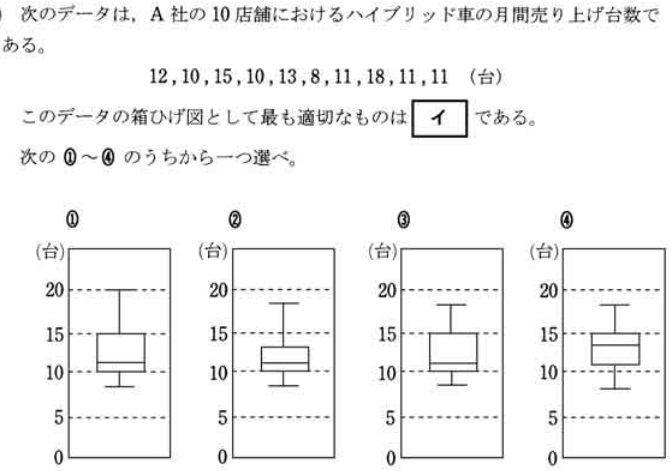
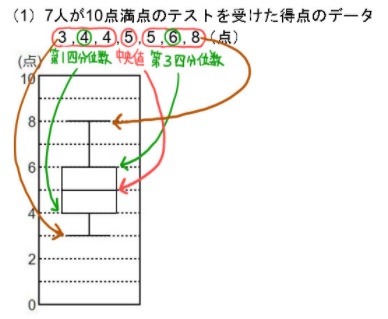
箱ひげ図を読み取る問題
令和元年
平成30年1
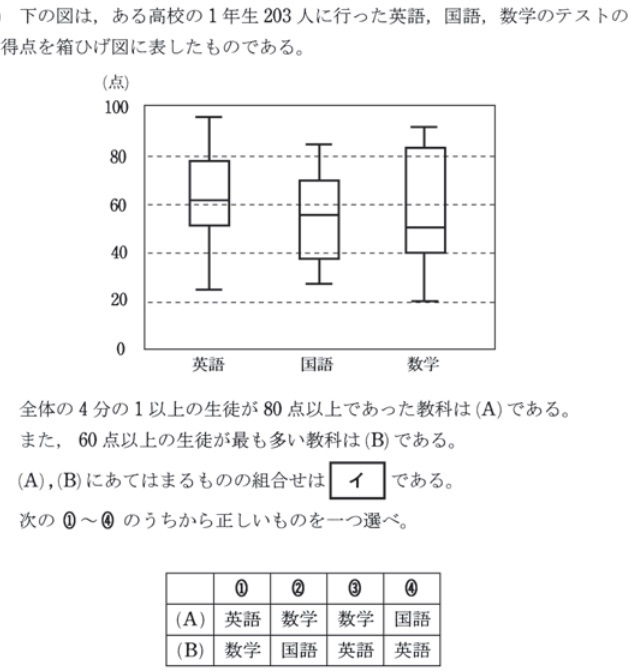
平成28年1
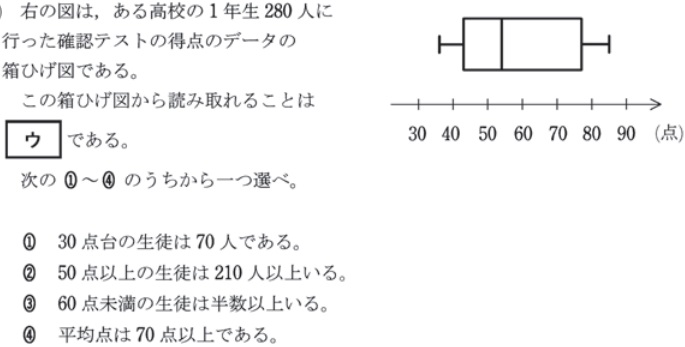
平均、分散、標準偏差の過去問パターン
にゃんこ
平均や分散や標準偏差について計算する問題です。分散や標準偏差の求め方については例年書かれていますが、計算事体が少し複雑になっています。対策問題の解答を見て、きれいに計算する手順を知って、反復練習で身に付けてください。
平均、分散、標準偏差
令和元年
平成30年
平成27年
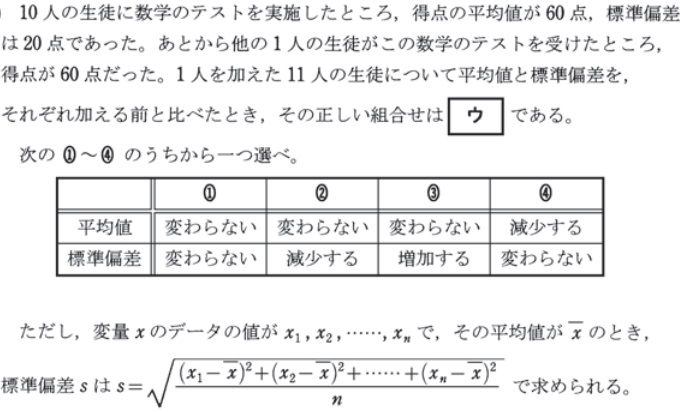
相関係数の過去問パターン
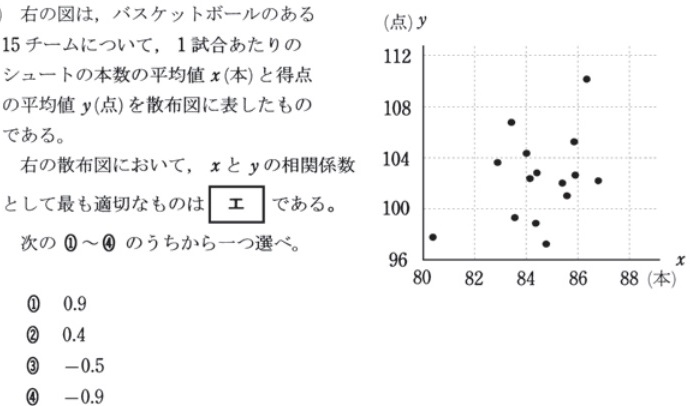
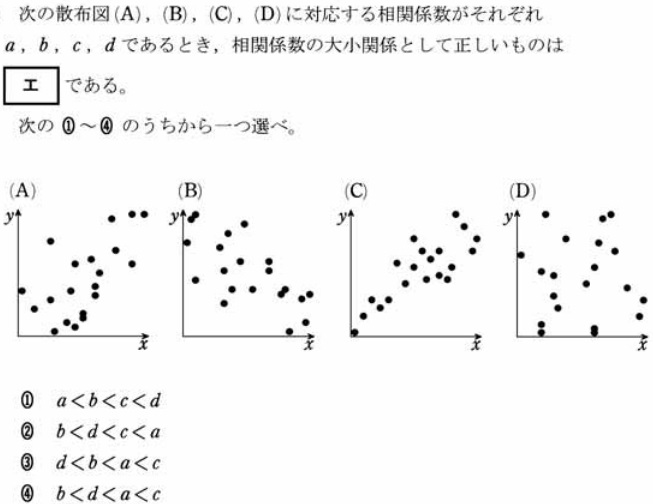
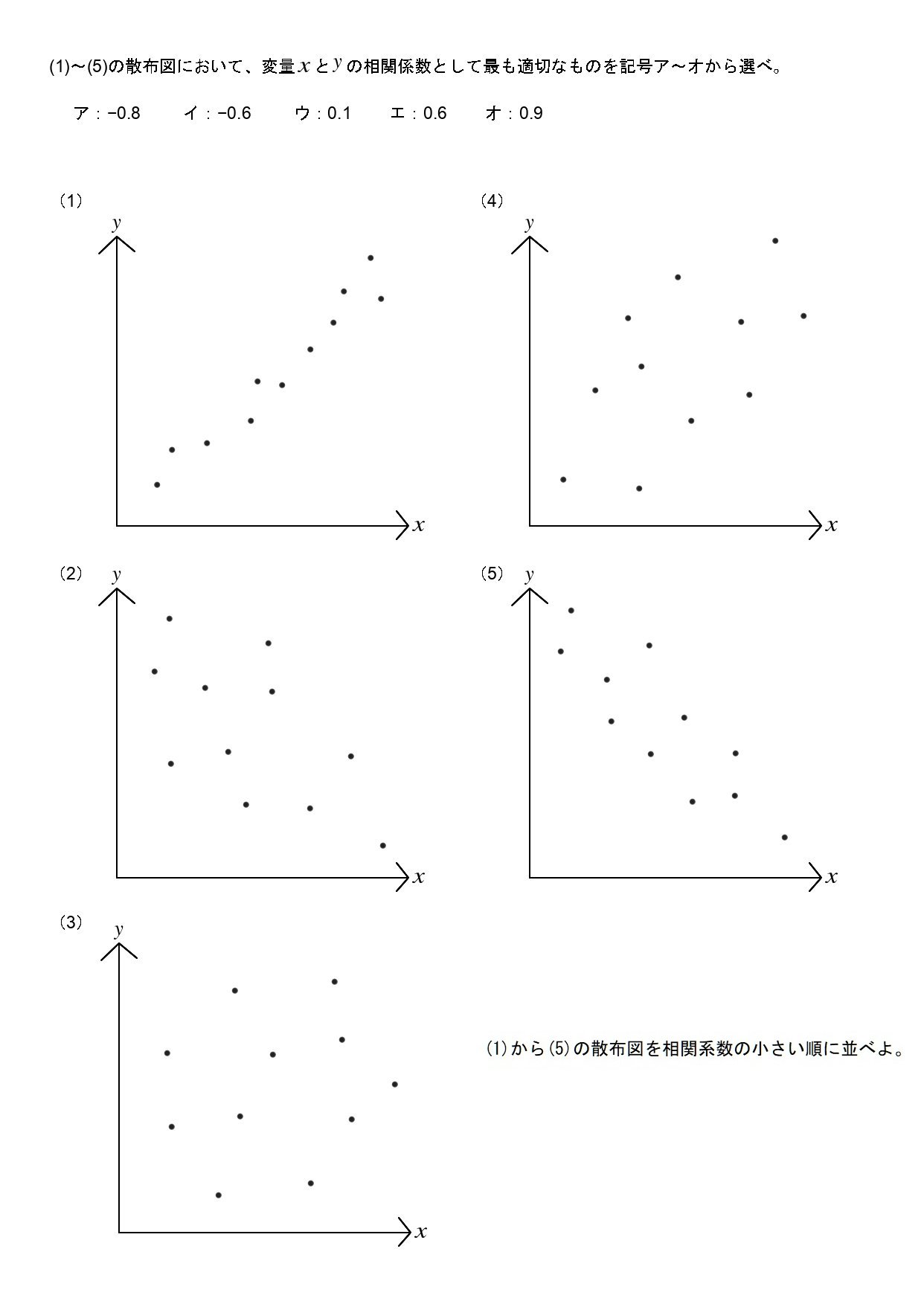
相関係数
坂田先生
相関係数は、正の相関や負の相関についての散布図の例を知っておくといいでしょう。過去問は基本的に、これを知っているかどうかを聞いています。
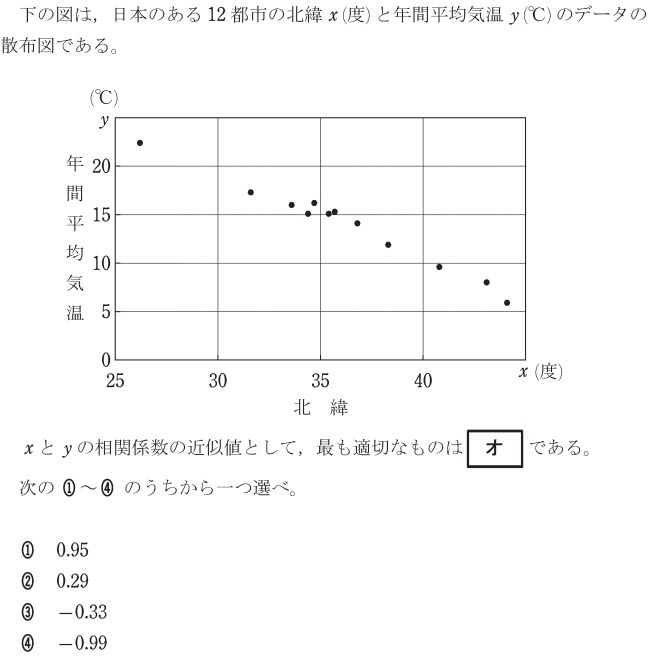
平成30年
平成29年
過去問の出題傾向の過去問パターン
坂田先生
高卒認定試験の数学は、過去問を見るかぎり、このような出題の傾向がみられます。
高卒認定試験数学｜過去問の出題傾向
高卒認定試験数学の過去問の解答・解説を読んでもわからない場合
にゃんこ
高卒認定試験数学の過去問の解答・解説を読んでもわからない場合の対応策について
解答・解説を読んでもわからない時
- 無料ですべて解決したい場合
無料コンテンツでその分野だけ調べるという方法です。
YouTube動画や記事を見て、高卒認定試験の数学を対策していくことは十分可能です。ただ、何をどう調べていいかわからなかったり、出題されない内容まで勉強してしまうというタイムロスが生じる可能性があります。 - ある程度有料でもいいので解決したい場合
参考書や有料授業や通信講座でわからなかった分野の解説を見る、という方法があります。
もっとも時間短縮になるのが、家庭教師やオンライン家庭教師を使い、わからなかった問題だけを質問するという方法です。
短期でもOKなところがあれば依頼するというのも手です。 - 中学数学から復習して、効果的な勉強方法まで教えてほしいという場合
勉強すべき内容からまるごと見てほしいという場合は、家庭教師にやオンライン家庭教師に頼むと効果が高いでしょう。
もちろん、依頼したからといってそれだけで実力はアップしません。
指示された勉強メニューをこなさない場合は効果はかなり低くなってしまいますので、それだけはご自身の心に聞いてみてください。
坂田先生
高卒認定試験の数学を独学で１から勉強する方は、こちら↓を読んでおいてください☆
にゃんこ
という方のために、無料部分たっぷりの講座をこちらに用意しました。
にゃんこ
高認数学講座たっぷり無料版をただ今プレゼント中★
詳細ページ：たっぷり無料版(失敗しない勉強方法解説付き)
坂田先生
中学数学の基礎から高認数学過去問レベルまで対策できる講座です。
数学が苦手な方のための高認数学講座
坂田先生のプロフィール
本名：坂田健太（滋賀県）１：訪問型の家庭教師
２：個別指導塾講師
を経験したのち、現在は
３：オンライン家庭教師
（指導歴はもうすぐ20年。100名以上指導)
として活動しています。
数学が苦手だった方のための高認数学講座
学習効率があまりよくない分野です。というのも、出題パターンが他の分野よりも少し多く、対策した分野が出題されない可能性があります。しかし、それでも２分の１ぐらいの確率ですので、過去問に出題されたものはどれも頻出パターンと言っていいでしょう。対策は必須です。
一次不等式の文章題だけは対策をあとまわしにしてもいいでしょう。バリエーションが少し多く、対策に時間がかかるかもしれません。対策をする場合は方程式の文章題の基礎を復習してからとりかかることをおすすめします。
二次関数と二次不等式は、基本が身に付けばいくつかの出題パターンがまとめて解けるようになるというお得な分野です。ただ、最初の基本を理解するのがほかの分野よりも難しいと感じるかもしれません。
いくつかの公式を覚えて、それをあてはめて解く、というただそれだけの分野です。代表的な三角比を覚えて解く問題がありますので、どんな暗記が必要かは、このページで公開しています。
データの分析は、高卒認定試験の数学のなかでも割とコスパがいい分野です。ただし、平均点や標準偏差を求めるときなど、計算ミスのしやすい場面がありますので、繰り返し解いてケアレスミスの対策をする必要があります。計算ミスのないように練習する時間がかかってしまうかもしれません。
つづいて、解説がわからない場合の対処法についてです。