

にゃんこ
※このページで掲載している問題の画像は、すべて坂田先生が過去問を研究し自作した、高認数学対策講座の問題です。(ここで紹介している参考書のものではありません)

坂田先生
ここでは高卒認定試験の数学の参考書『高卒認定ワークブック改訂版 新数学』の最も効果的な使い方について解説します。

にゃんこ
実はこのテキスト、効果的に使える部分とけっこう使えない部分があるのを知っていましたか?

坂田先生
この参考書でカバーしきれていない部分に関しては、僕の講座↓で対策できるようにしています。
高卒認定試験の数学|独学用の参考書とテキストの使い方

坂田先生
過去に実際に出題された問題と照らし合わせて、使える部分と、効果の薄い部分とを仕分けしました。

にゃんこ
さきほども言いましたがこの参考書。単元によっては、対策のための問題が少ないという部分もあります。

坂田先生
この参考書の目次にそって使い方をご説明します。
第1章 数と式
第2章 2次関数
- 関数の基礎
参考書のここの内容は近年出題されていません。とばしてください。 - 2次関数とグラフ(1)
中学3年生で習う二次関数の復習です。
高卒認定試験の数学で実際に出題される内容は次の項目からになりますが、グラフの向き(上に凸のグラフか下に凸のグラフか)などは引き続き使うので、テキストのそのあたりだけ読んでおくといいでしょう。 - 2次関数とグラフ(2)
ここの練習問題はとても有効です。グラフの頂点を求める問題やグラフを平行移動させる問題は頻出なので、よく練習しておきましょう。 - 2次関数とグラフ(3)
こちらも引き続きグラフの頂点を求める問題と、さらにy切片と軸について求める問題です。
y切片と軸について求めるテクニックはたしかに使う場面もなくはないですが、高卒認定試験の数学ではあまり出題されていないので、最初はとばしておいて大丈夫です。 - 2次関数の最大値・最小値
この内容も頻出です。しかし、基礎問題に掲載されている問題のパターンがそのまま出題されたためしはありません(これは中学数学の内容なので)。
レベルアップ問題がよく出る形式です。
ただし、いきなりレベルアップ問題をするのではなく、基礎問題の練習をしてからとりかかると、理解もしやすいかと思います。 - 2次関数とグラフと2次方程式
二次関数のグラフとX軸との共有点についての問題を練習します。よく出ます。
共有点の個数と、共有点の座標の両方を答えられるようにしてください。(共有点の座標を問われることのほうが多いです) - 2次関数とグラフと2次不等式
二次不等式の解を求める問題です。よく出ます。テキストにある練習問題がちょうどいい対策になっています。
ただし解説がグラフなしなので、読んでもサッパリわからない可能性があります。
こんなふうにグラフも添えて説明してほしかった。 

第3章 図形と計量
- 直角三角形と三角比
ここのレベルアップ問題がよく出ます。基礎問題はそのまま出ることはありませんが、三角比の基礎なので練習しておいてください。 - 三角比の相互関係
基礎問題はほぼ出題されていません。レベルアップ問題は出題されている形式のものもありますが、問題数が少ないです。こちらで練習してください。

- 三角比の拡張
ここの最初の説明のページにある三角比の値が表になったものを暗記してください。使います。
この表のことです。暗記してください。(※これは僕の高認対策オリジナルプリントです。) 
この部分と、参考書の基礎問題とレベルアップ問題を解いておいてください。 - 正弦定理と余弦定理
正弦定理と余弦定理はよく出ます。テキストに書かれている公式を暗記し、基礎問題、レベルアップ問題で対策すれば身に付くでしょう。
ただ、余弦定理は三角形以外でも実際に出題されているので、そのための対策としてこの問題を解いておいてください。(この参考書では三角形オンリーの練習しかできません。)
これを使って、三角形以外のかたちでも対応できるように練習しておいてください。 
- 三角形の面積と三角比
三角比を使った面積を求める問題です。よく出ます。しかし、これもまたこの参考書では三角形しか練習できません。
参考書の問題で練習+こちらのプリントで三角形以外の形にも応用できるよう準備しておいてください。
三角形以外にも対応できるオリジナルプリント 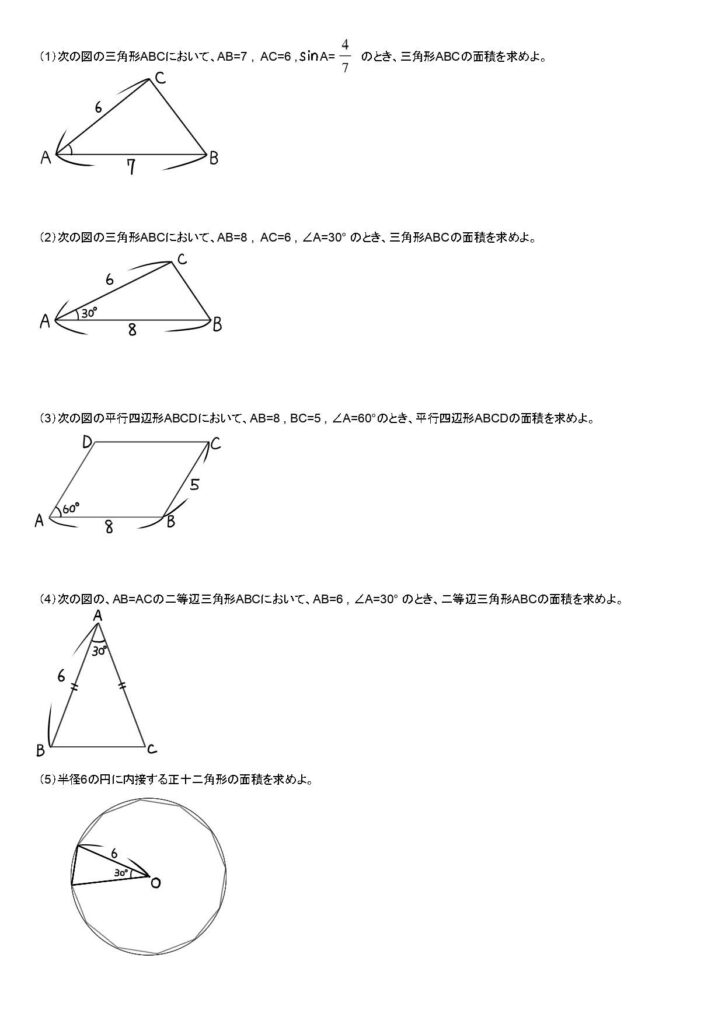
第4章 データの分析
- データと度数分布表
高速認定試験の数学において、データの分析の最初の問題は、各用語の意味を理解しているかどうかがよく問われます。ヒストグラムやデータを見て
最大値
第3四分位数
中央値
第1四分位数
最小値
範囲
最頻値
平均値について質問してくる問題です。
これらの意味を理解するには、この参考書の次の章【代表値/散らばりを表す数値】まで読んでおく必要があります。
ここの単元の基礎問題やレベルアップ問題はそのまま高卒認定試験の数学で出題されることはないですが、解答できるぐらいの理解はしておいてください。次で使います。 - 代表値/散らばりを表す数値
この基礎問題とレベルアップ問題は出題されます。ただ、実際にはレベルアップ問題の形式で出題されることがほとんどなので、問題のバリエーションが少ない気がします。
練習できたら過去問とこちらの練習プリントで練習しておいてください。 - 分散・標準偏差/相関関係と相関係数
ここは手間のかかる平均・分散・標準偏差を求める計算の練習をしなければなりませんが、この参考書では用語を問う形式がほとんどで問題が少なすぎます。分散や標準偏差の公式は暗記する必要はなく、過去問を見ればたいてい公式が掲載されています。
この単元では計算ミスをしない練習をするために時間を使ってください。
こんな感じで計算ミスをしない練習をしてください。 
 ※高速認定試験数学の出題傾向として、平均と分散と標準偏差のどれかが毎年のように出題されています。
※高速認定試験数学の出題傾向として、平均と分散と標準偏差のどれかが毎年のように出題されています。
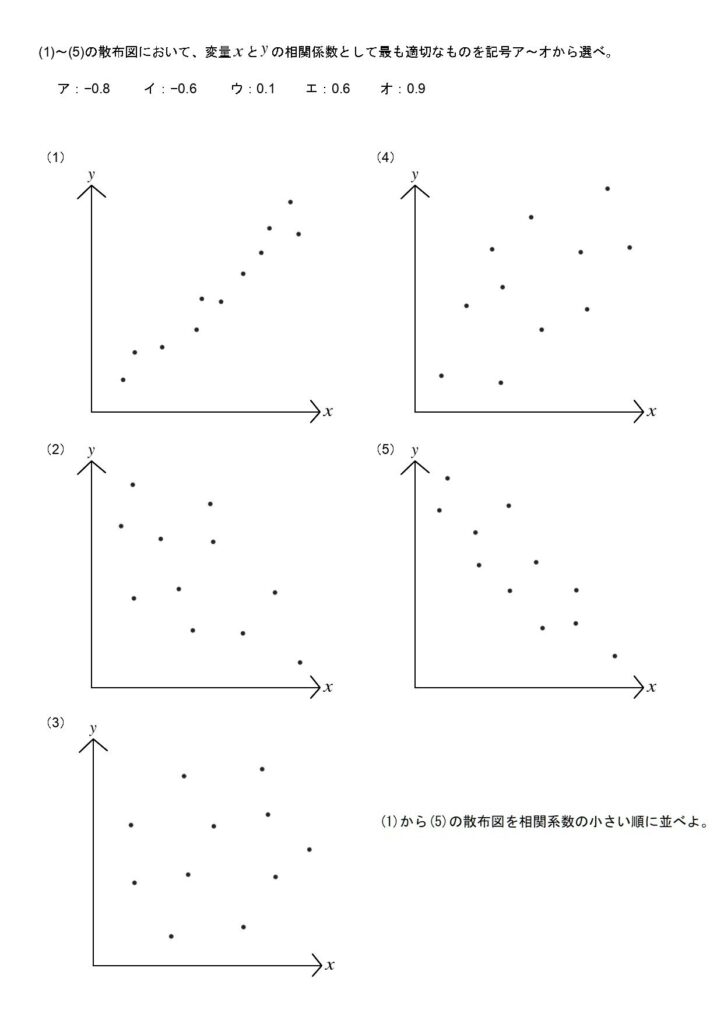
また、正の相関、負の相関に関する理解を問う問題が最後に出題されています。
ここの対策問題も少なかったので、こちらも練習プリントを併用してください。

坂田先生
高卒認定ワークブック改訂版 新数学の感想レビュー

坂田先生
さいごにこの書籍の感想を述べておわります。
- よかった点
単元によっては、ばっちり出題傾向と問題のレベルが合致していて、十分対策できる内容となっている。中学数学から復習させる単元もあり、その点は評価できる。 - 改良してほしい点
最新の高卒認定試験の数学の出題傾向に合わせた問題編成に改善してほしい。単元によっては練習問題が少ない、問題が簡単すぎて使えないなどのズレが生じている。 - 映像授業に関して
この参考書、映像授業のコンテンツが別に販売されていますが、僕はこれはまだ見たことがないので、コメントは差し控えさせていただきます。参考書の解説の不足分をこれでカバーできているなら使用価値はあるでしょう。















































 本名:坂田健太(滋賀県)
本名:坂田健太(滋賀県)
高速認定試験数学では、平方根の問題が出題されていますので、その対策としてこの単元を使用します。
レベルアップ問題に、有理化の問題がありますので、参考書ではそれができるかどうかだけを優先的に対策して他はあとまわしにしてください。(近年の過去問を見る限り、ほとんど不要です)
部分集合や補集合といった概念の説明が最初にあります。これは読んでおいてください。よく出ます。
練習問題は、頻出の形式がほとんどないので、テキストで概念を理解したら、こちらの頻出パターン問題を使用してください。
命題の真偽や、必要条件、十分条件についての問題を対策するところですが、3つの理由によりとばしておいてください。
理由1:最初の理解がすこし難しい。
理由2:この参考書では、この単元の過去の出題パターンに沿った練習問題が少なすぎる。
理由3:出題問題にバリエーションがあり、対策に時間がかかる可能性があり、コスパが悪い。
この参考書では、因数分解や、式の展開について、最初に公式が列挙されています。
実際に使用するのはそのほんの一部なので、まず最初にそのテキストにある練習問題の問題と解答を見ながら、使用する公式のみにマーカーをひいておきましょう。
因数分解は、たすきがけが出題のほとんどです。
展開の練習問題が少ないので、実際の過去問を練習するか、僕のオリジナル問題を使ってください。
1次不等式は高速認定試験の大問2の1と大問2の2で出題されています。
大問2の1では
1:カッコつきの一次不等式
2:小数つきの一次不等式
3:分数つきの一次不等式
大問2の2では
一次不等式の文章題
が出題されています。
ところがこの参考書では
1:カッコつきの一次不等式
2:小数つきの一次不等式
3:分数つきの一次不等式
のどれも練習問題にのっていません。
その前提となる基本の解き方を練習する問題が掲載されているだけです。
これはこれで練習になるのですが、その状態では点数にならないので、こちらの問題を練習してください。
また、一次不等式の文章題は一題だけテキストに掲載されています。
大問2では毎年のように出題されていますが、個人的にはここは後回しにすることをおすすめします。
理由は、文章題が苦手な場合、対策に時間がかかるからです。文章題は内容にバリエーションもあります。
これを対策する場合、中学数学の方程式の文章題(中1)を復習してからのほうがいいでしょう。